Selbst tödliche Krankheiten haben was mit Mathe zu tun, denn der Grund, weshalb Bakterien so gefährlich sind, ist ihr exponentielles Wachstum. Ihre Anzahl nimmt im Körper nicht immer um denselben Betrag zu, sondern sie wachsen immer schneller. Hier erklären wir euch die mathematischen Hintergründe dazu.

Bakterien sind für unseren Körper so gefährlich, da sie sich in ihm exponentiell vermehren, das bedeutet, es kommt nicht immer dieselbe Anzahl in einer gewissen Zeit hinzu, sondern immer mehr in derselben Zeit. Deshalb lässt sich ihr Wachstum als Exponentialfunktion beschreiben. Wir wollen es euch anhand der E.-Coli-Bakterien veranschaulichen. Ihre Anzahl verdoppelt sich alle 20 Minuten im Körper.
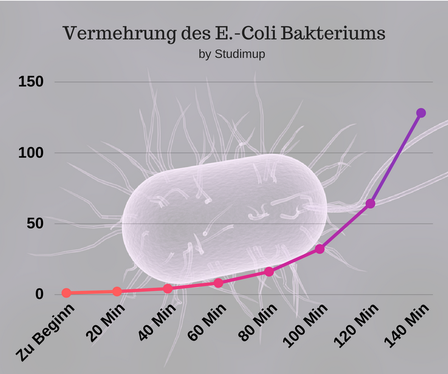
Hier seht ihr, wie die Anzahl der E.-Coli Bakterien steil zunimmt und immer schneller wächst. Wenn man mit einem Bakterium beginnt, sind es nach nur 140 Minuten schon 128!
Da man weiß, dass sich die Anzahl der E.-Coli-Bakterien alle 20 Minuten verdoppelt, kann man leicht die Exponentialfunktion erstellen:

- N0 ist die Anzahl von Bakterien am Anfang
- t ist die Vergangene Zeit in Minuten
- N ist die Anzahl nach der Zeit t mit dem Anfangsbestand N0
Mit dieser Geleichung ergibt sich folgender Graph:
| Vergangene Teit t | Anzahl Bakterien N |
| 0 Min | 1 |
| 20 Min | 2 |
| 40 Min | 4 |
| 60 Min | 8 |
| 80 Min | 16 |
| 100 Min | 32 |
| 120 Min | 64 |
| 140 Min | 128 |
| 3 Stunden | 512 |
| 4 Stunden | 4096 |
| 5 Stunden | 32768 |
| ..... | ..... |
| 12 Stunden | 68719476740 = 6,87·1010 |
| 24 Stunden | 4,72×1021 |
Wie ihr seht, sind es bereits 4,72×1021 Bakterien, nach nur einem Tag! Und 20 Minuten später noch mal doppelt so viele! An diesem Beispiel erkennt ihr, welche Wirkung ein exponentielles Wachstum haben kann. Deshalb sollte man immer wissen, was gemeint ist, wenn jemand von exponentiellem Wachstum spricht.





