Wie berechnet man die durchschnittlichen Kosten für ein Panini-Sammelalbum?

Viele Fußballfans sammeln leidenschaftlich Panini-Sticker zur WM 2018. Die wenigsten fragen sich jedoch, wie viel ein volles Album in etwa kostet und wie viele Sticker man kaufen muss, bis man jeden mindestens einmal hat. Studimup zeigt euch, wie viele Bildchen und Packungen ihr im Durchschnitt braucht, um ein vollständiges Sammelalbum zu haben und wie viel dieses dann ca. kostet. Natürlich zeigen wir euch auch, wie man das berechnet.

Berechnung der Kosten für ein volles Sammelalbum an Panini-Stickern.

Die Berechnung

Wie ihr sicherlich wisst, gibt es 682 verschiedene Sticker. Um nun zu berechnen wie viele ihr im Durchschnitt benötigt, bis ihr alle habt, müsst ihr wie folgt rechnen:

Zunächst berechnet man die Anzahl an Stickern, die man kaufen muss, bis man im Durchschnitt jeden mindestens einmal hat (man tut so, als würde man die Sticker einzeln kaufen). Danach kann man es in Tüten umrechnen (würde man gleich in Tüten rechnen, würde es zu Ungenauigkeiten kommen).

Ihr wisst, dass die Wahrscheinlichkeit (Laplace Experiment) ein bestimmtes Bildchen zu ziehen folgende ist (eins durch die gesamte Anzahl):

Um also ein fehlendes Bildchen zu ziehen, müsst ihr im Durchschnitt 682 Sticker kaufen (umstellen der Formel):

Wenn euch noch zwei Sticker fehlen berechnet ihr das genauso, nur dass ihr eine 2 statt einer 1 in den Bruch schreibt (dies ist dann die Wahrscheinlichkeit dafür, einen fehlenden Sticker zu kaufen, wenn euch noch zwei fehlen):

Also müsst ihr im Durchschnitt 341 Sticker kaufen, bis ihr einen der beiden fehlenden Sticker habt. Dies könnt ihr dann so weiterführen, also wenn euch noch 3 fehlen, wie viele ihr kaufen müsst, bis ihr einen davon habt, wenn 4 fehlen usw. (sozusagen Rückwärts rechnen, denn eigentlich fehlen euch ja erst 682, dann 681, ... , dann 2, dann 1) :

Ihr addiert also die Anzahlen an Stickern, die ihr kaufen müsst, um einen neuen zu bekommen, wenn euch noch einer fehlt, zwei fehlen, drei fehlen, vier fehlen... bis zum Anfang, wo euch noch alle fehlen (also 682). Wie ihr sehen könnt, ergibt der letzte Bruch 1, dass ist auch logisch, denn wenn euch noch alle 682 Sticker fehlen, dann müsst ihr nur einen Sticker kaufen, bis ihr einen neuen habt. Dies kann man nun auch anders schreiben, nämlich in der Summenschreibweise (bedeutet dasselbe, wie die Schreibweise darüber):

Berechnet man nun diese Summe, kommt man auf folgendes Ergebnis:

Also muss man im Durchschnitt 4844 Sticker kaufen, bis man jeden einmal hat. Nun kann man das noch in Tüten ausrechnen, indem man durch 5 teilt (in einer Tüte sind ja 5 Sticker):

Also braucht man ca. 969 Tüten bis man alle Bildchen mindestens einmal hat. Dies bedeutet man muss im Durchschnitt 872,10€ Zahlen, wenn eine Tüte 90 Cent kostet:

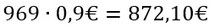
Das sind die durchschnittlichen Kosten für ein Panini-Sammelalbum. Wie gesagt ist dies nur der Durchschnitt, man kann auch weniger brauchen, wenn man Glück hat, oder mehr, wenn man Pech hat.