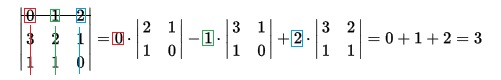Laplace Entwicklungssatz
Mit dem Laplace Entwicklungssatz kann man einfacher und schneller Determinanten von großen Matrizen berechnen, als mit der eigentlichen Definition der Determinate. Es lassen sich dann Deternimanten von 4x4, 5x5... nxn Matrizen leicht lösen.
Schritt für Schritt
Beim Laplace-Entwicklungssatz geht ihr so vor:
- Sucht euch eine Zeile oder Spalte aus, welche möglichst viele 0en hat. Es ist egal welche Zeile oder Spalte ihr nehmt, es kommt immer dasselbe raus! Streicht diese Zeile oder Spalte durch.
- Jetzt streicht ihr nacheinander jede Spalte durch, wenn ihr euch zuerst eine Zeile ausgesucht habt. Habt ihr zuerst eine Spalte ausgesucht, streicht ihr Zeilen durch. Immer der Teil, der nicht durchgestrichen ist, ist die "neue" Matrix, von der die Determinate bestimmt wird.
- Die Zahl, die dann in der durchgestrichenen Zeile und Spalte liegt, wird dann mal die Determinante genommen.
- Das macht ihr jetzt genauso weiter, indem ihr die nächste Zeile bzw. Spalte durchstreicht, bis ihr alle durchseid. Dann addiert bzw. subtrahiert ihr eure Ergebnisse, die ihr so bestimmt. Ob ihr addiert oder subtrahiert findet ihr so raus:
- immer die Zahl ganz oben links ist +. (Also wenn ihr diese Zahl mal die Determinante nehmt, wird dies Addiert)
- dann die nächste rechts daneben ist - (Steht diese Zahl vor der Determinante, wird also subtrahiert), dann wieder + und dann - usw.
- die nächste unter der ganz oben rechts ist -, dann die nächste darunter + und dann wieder - usw.
Beispiel 1:
- Zunächst wurde die 1. Zeile ausgewählt, da dort eine 0 ist
- Nun streicht ihr nacheinander die Spalten durch. Immer das, was nicht durchgestrichen ist, ist dann die "neue" Matrix von der ihr die Determinate bestimmt. Hier wurde erst die rote Spalte durchgestrichen. Der Rest ist dann die "neue" Matrix.
- Die Zahl, die dann in der Durchgestrichenen Spalte und Zeile ist, nehmt ihr dann mal die neue Determinante. (Jetzt seht ihr, warum man eine Spalte bzw. Zeile zuerst raussucht, die möglichst viele 0-en hat, da so viel wegfällt)
- Jetzt die nächste Spalte durchstreichen und das ganze nochmal. Nicht vergessen, dass die Zahl rechts von der ganz oben links ein - bekommt, weshalb ihr das dann minus die vorherige Determinate macht (hier die grüne 1).
- So geht ihr vor, bis ihr alle Spalten durch habt. Dann könnt ihr die Determinanten mit der Kreuzregel berechnen. (Oben links mal unten rechts - oben rechts mal unten links)
Beispiel 2:
- Hier wurde zunächst die erste Spalte durchgestrichen.
- Dann wurden nacheinander, wie oben beschrieben, die Zeilen durchgestrichen
- Die so neu entstandenen Matrizen werden immer mal die Zahl genommen, die in der durchgestrichenen Zeile und Spalte liegen.
- Vergesst nicht, dass die Zahl unter der ganz oben links, immer - genommen wird. Hier spielt es allerdings keine Rolle, da es eine 0 ist.
- Berechnet so die kleineren Matrizen und ihr erhaltet dann die Determinante.
Blog
Studimup Mathe-Lernmaterial
Einfach Mathe lernen mit den Lernmaterialien von Studimup❗ Die Lernkarten "Spickzettel A6" 📄 und die Bücher "Mathe für dich" 📚 erleichtern das Lernen und Wiederholen von Mathematik. 😎
