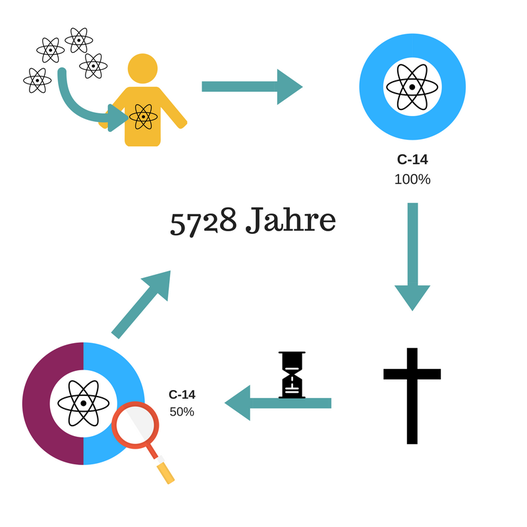
Woher weiß man, wie alt Mumien sind? Und woher wusste man, wann der Ötzi gestorben ist? Natürlich dank der Mathematik (und Physik). Im Körper ist nämlich eine bestimmte Menge an radioaktivem Kohlenstoff, auch C-14 genannt, welches nach dem Tod exponentiell abnimmt. Daher wird diese Methode auch C-14 oder Radiokarbonmethode genannt.

Bestimmung des Alters
In unserer Umgebung kommt eine gewisse Menge an radioaktivem Kohlenstoff, sogenanntem C-14 vor (wird so genannt, da es nicht wie der "normale" Kohlenstoff aus 12 Kernbausteinen besteht, sondern aus 14), das Verhältnis von gewöhnlichem C-12 und C-14 ist auf der Erde seit Jahrtausenden (fast) immer gleich geblieben. Essen nun Lebewesen etwas, atmen oder haben anderen Stoffwechsel, nehmen sie ganz natürlich dieses C-14 zu sich. Sobald sie aber sterben ja nicht mehr, sodass auch kein "frisches" C-14 aufgenommen wird. Da nun das C-14 radioaktiv ist, zerfällt dieses, wodurch in den Überresten immer weniger C-14 ist. Alle 5728 Jahre zerfällt die Hälfte des C-14. Hat man dann einen Knochen (oder etwas anderes von einem Lebewesen), kann man durch das Verhältnis von C-12 und C-14 das Alter bestimmen, je älter die Probe ist, desto mehr nicht radioaktiven Kohlenstoff gibt es im Vergleich zum radioaktiven C-14. Diese Eigenschaft macht sich die Radiokarbonmethode zu Nutzen.
Um nun das Alter berechnen zu können, muss man aus dem Material, von welchem das Alter bestimmt werden soll, den Kohlenstoff extrahieren (also vom Rest trennen) und dann wird mit der Aktivität (also wie viele Kernzerfälle in einer gewissen Zeit stattfinden) festgestellt, wie viel C-14 im Vergleich zum restlichen Kohlenstoff noch vorhanden ist. Dabei muss man darauf achten, dass sich die Menge die Menge an C-14 nicht proportional, sondern exponentiell ändert, dadurch wird die Berechnung etwas komplizierter. Alle 5728 Jahre ist die Hälfte vom C-14 zerfallen. Dann kann man mit dieser Formel das Alter eines Knochens oder anderen organischen Materials festgestellt werden:

- VK ist das Verhältnis von C-14 zu C12, also das Verhältnis der Kohlenstoffisotope im Knochen
- VL ist das Verhältnis von C-14 zu C12 in der Luft/Umgebung, also das Verhältnis der Kohlenstoffisotope in der Umgebung, als das Lebewesen noch gelebt hat (ist (fast) gleich dem Verhältnis von heute).
- e ist die Eulersche-Zahl
- λ erhält man, indem man den natürlichen Logarithmus von 2 bildet und dieses Resultat durch die Halbwertszeit dividiert. Die Halbwertszeit von Kohlenstoff (C-14) beträgt ca. 5730 Jahre. Also das ist die Zeit, nach der die Hälfte vom C-14 zerfallen ist. Der Wert von λ ist 1,21·10-4 1/a
- t ist die Zeit, die Vergangen ist
Jetzt kann man die Formel umformen, sodass man die Zeit berechnen kann, dabei benötigt man den natürlichen Logarithmus:



Jetzt mal ein Beispiel. In der Luft ist ca. 10−10 % des Kohlenstoffs C-14, der Rest ist nicht radioaktiver Kohlenstoff. Jetzt hat man eine Mumie gefunden, in welcher 0,5·10-10% des Kohlenstoffs C-14 ist. Das setzt ihr alles zusammen mit λ (=1,21·10-41/a) ein, und ihr erhaltet das Alter der Mumie in Jahren:

Also ist die Mumie, welche gefunden wurde, ca. 5728,5 Jahre alt.
Genauigkeit (Standardabweichung)
Um die Genauigkeit einer Messung anzugeben und zu bestimmen, berechnet man die Standardabweichung. Mithilfe dieser kann man dann angeben, in welchem Zeitraum das Lebewesen oder die Pflanze, welche man untersucht hat, gestorben ist. Dazu fertigt man mehrere Proben und Messungen des Verhältnisses von C-14 und C-12 an und setzt die Ergebnisse dann in die Formel für die Standardabweichung ein. Das, was rauskommt, schreibt man dann mit einem ± an das Ergebnis dran. Meist sind die Messungen auf ±30 bis ±50 Jahre genau. Mit dem Beispiel von oben wäre es also (wurde aber nicht berechnet, nur als Beispiel, wie man es aufschreibt) 5728±40 Jahre.
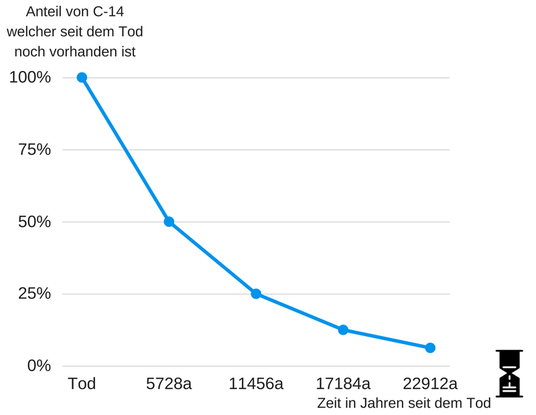
Man kann allerdings diese Methode zur Altersbestimmung nicht unbegrenzt anwenden, denn dafür ist die Halbwertszeit von C-14 zu kurz. Um verlässliche Daten zu erhalten, muss die Probe jünger als 60.000 Jahre sein, da sonst keine verlässlichen Daten mehr möglich sind. Das liegt mit daran, dass es eine exponentielle Abnahme ist, diese fällt immer flacher ab, sodass ab einem bestimmten Alter der Probe die Unterschiede des Verhältnisses so gering werden, dass kein Alter mehr zuverlässig angegeben werden kann.
Hier seht ihr eine Grafik, die euch zeigt, wie die Menge an C-14 ab dem Tod eines Lebewesens abnimmt. Alle 5728 Jahre zerfällt die Hälfte des C-14: