Stochastische Unabhängigkeit
Stochastische Unabhängigkeit bedeutet, dass ein Ereignis das nachfolgende Ereignis in seiner Wahrscheinlichkeit nicht beeinflusst. Das heißt, dass egal was vorher passiert, die Wahrscheinlichkeit für das Ereignis danach bleibt gleich, zum Beispiel, wenn man eine Münze zweimal wirft, der erste Wurf verändert die Wahrscheinlichkeit vom 2. Wurf nicht, diese bleibt weiter bei 50% Kopf oder Zahl, daher ist das stochastisch unabhängig. Allgemein gilt Folgendes für stochastische Unabhängigkeit:


Mit der Formel könnt ihr eine Wahrscheinlichkeit auf stochastische Unabhängigkeit überprüfen (Beispiele dazu sind unten). Wenn also die "Undwahrscheinlichkeit" gleich dem Produkt der Einzelwahrscheinlichkeit ist, ist es stochastisch unabhängig.
Daraus folgt, wenn einer der beiden Fälle zutrifft, ist es stochastisch unabhängig (zum Thema Baumdiagramm):
a) Wenn folgende Gleichung stimmt:

b) Wenn P(B) (die Wahrscheinlichkeit, dass B eintrifft) an beiden Ästen zu Ereignis B gleich ist:

Beispiel stochastische Unabhängigkeit
Man wirft 2 mal eine Münze. Sind die Wahrscheinlichkeiten stochastisch unabhängig, ob beim zweiten Wurf Kopf (K) oder Zahl (Z) rauskommt?

Wie ihr seht, ist die Wahrscheinlichkeit, dass Kopf geworfen wird auf beiden Seiten gleich, deshalb ist diese Wahrscheinlichkeit stochastisch unabhängig.
Man kann es auch mit den Formeln von oben berechnen:
P(K∩Z)=P(K)·P(Z)
0,25=0,5·0,5 ✓
Beispiel stochastische Abhängigkeit
Man zieht aus einer Urne mit 10 Kugeln, wobei 6 rot und 4 grün sind, nacheinander 2 Kugeln. Dabei wird nach dem ersten ziehen die Kugel nicht wieder zurückgelegt. Ist die Wahrscheinlichkeit beim zweiten Ziehen stochastisch abhängig, zu dem was zuerst gezogen wurde?
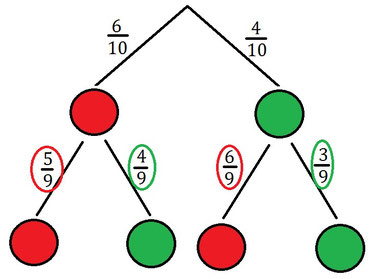
Wie ihr seht, sind die Wahrscheinlichkeiten rot oder grün beim zweiten mal zu ziehen jeweils unterschiedlich, je nachdem, was davor gezogen wurde. Deshalb sind die Wahrscheinlichkeiten stochastisch abhängig. Das könnt ihr auch rechnerisch zeigen (R=rot; G=grün):
P(R∩G) ≠ P(R)·P(G)
0,27 ≠ 0,6·0,4
Beispiele für stochastische Unabhängigkeit:
- Münzwurf, denn wenn man Kopf wirft, beeinflusst es nicht die Wahrscheinlichkeit beim nächsten Wurf
- Würfeln, wenn man einmal gewürfelt hat, ändert dies ja nicht die Wahrscheinlichkeit beim nächsten Würfeln.

Beispiel für stochastische Abhängigkeit:
- Ziehen von Kugeln ohne zurücklegen, da wenn man eine herausgezogen hat sich die Wahrscheinlichkeit beim nächsten Ziehen ändert.
- Lotto 6 aus 49, da wenn eine Zahl schon gezogen wurde, ändert sich die Wahrscheinlichkeit für die nächste Kugel.

Aufgabe zur stochastischen Unabhängigkeit
Hier eine Aufgabe mit der ihr selbst üben könnt. Klickt auf einblenden für die Lösung.
| Ihr zieht 3 Kugeln aus einer Urne und legt sie nach jedem Ziehen zurück. Ist diese Wahrscheinlichkeit eine Kugel nach dem ersten Ziehen stochastisch unabhängig oder abhängig? | Einblenden | |
|
Lösung: Diese Wahrscheinlichkeit ist stochastisch unabhängig, da sich die Wahrscheinlichkeit nach dem ersten ziehen nicht ändert, da wieder gleich viele Kugeln in der Urne liegen. |
||
