Bedingte Wahrscheinlichkeit
Die bedingte Wahrscheinlichkeit ist die Wahrscheinlichkeit eines Ereignisses unter der Bedingung, dass davor ein anderes Ereignis zugetroffen ist. Sie ist von dem vorherigen Ereignis abhängig, wenn davor ein anderes Ereignis zutrifft, kann sich die Wahrscheinlichkeit verändern. Es ist also eine "wenn..., dann..." Beziehung.
PA(B)
Geschrieben wird die Wahrscheinlichkeit von B unter der Bedingung, dass A eingetroffen ist, wie hier gezeigt.
Beispiel:
Wenn man gelernt hat, mit welcher Wahrscheinlichkeit bekommt man eine 1?
- Die Bedingung ist, dass man gelernt hat, steht also da, wo das A steht.
- Die Wahrscheinlichkeit, die man berechnen möchte, ist, dass man eine 1 bekommt, wenn man gelernt hat. Das ist das B.
Wie ihr auch an dem Beispiel seht, beeinflusst das Ergebnis davor die Wahrscheinlichkeit für das danach, denn wenn man nicht lernt, ist die Wahrscheinlichkeit eine 1 zu bekommen deutlich geringer.
Die bedingte Wahrscheinlichkeit findet ihr im Baumdiagramm an dieser Stelle:
Die bedingte Wahrscheinlichkeit berechnet ihr folgendermaßen (durch Umstellung könnt ihr auch die anderen Wahrscheinlichkeiten ausrechnen):
- P(A∩B) ist die Wahrscheinlichkeit, dass A und B eintreffen, es ist die sogenannte "Undwahrscheinlichkeit". Mit dem Beispiel von oben wäre es also die Wahrscheinlichkeit, dass jemand gelernt hat und eine 1 bekommt.
- P(A) ist die Wahrscheinlichkeit für A, also die Wahrscheinlichkeit, dass die Bedingung zutrifft. Mit dem Beispiel von oben wäre es, dass jemand gelernt hat.
Beispiel: bedingte Wahrscheinlichkeit berechnen
Von 40 Leuten sind 6 farbenblind. 4 dieser Leute sind Männer und farbenblind. Wie groß ist die Wahrscheinlichkeit, dass wenn eine Person farbenblind ist, diese dann ein Mann ist?
Lösungsschritte:
- Schaut was als Erstes zutreffen muss, das ist dann die Bedingung, also hier, dass die Person farbenblind ist. Ihr möchtet ja wissen, dass wenn eine Person farbenblind ist, mit welcher Wahrscheinlichkeit sie dann ein Mann ist.
- Berechnet den Anteil an Leuten, die männlich und farbenblind sind, also beide Bedingungen erfüllen. Also die 4 Männer, die farbenblind sind, durch die Gesamtanzahl an Leuten (4/40). So habt ihr P(A∩B).
- Dann berechnet ihr die Wahrscheinlichkeit der Bedingung, also dem, was zuerst zutreffen muss. Hier also die Wahrscheinlichkeit, dass eine Person farbenblind ist (egal ob Mann oder Frau). Dafür Teilt ihr die Farbenblinden durch die Gesamtanzahl (6/40).
- Dann teilt ihr die beiden Ergebnisse und erhaltet die bedingte Wahrscheinlichkeit (also die, dass beides zutrifft und die, dass die Bedingung zutrifft), hier in dem Fall sind es 66,7%. Ihr könnt dies als Übung nachrechnen.
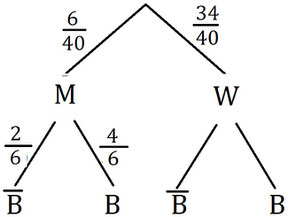
Hier seht ihr das passende Baumdiagramm zu dieser Aufgabe. Dabei steht M für männlich, W für weiblich, B für farbenblind und B strich/nicht für nicht farbenblind.
Wie ihr seht, sind die bedingten Wahrscheinlichkeiten nach der Bedingung und ergeben zusammen 1, also 100%, denn die Männer sind ja entweder farbenblind oder nicht, also trifft eins von beidem sicher zu. Die Wahrscheinlichkeiten sind dann 2/6 für nicht farbenblind, da 2 von den 6 Männern nicht farbenblind sind und 4/6 das jemand männlich und farbenblind ist, da 4 von den 6 Männern farbenblind sind.
Aufgabe zur bedingten Wahrscheinlichkeit
Klickt auf einblenden, um die Lösung der Aufgabe zu sehen.
| Schüler einer Klasse mit 30 Schülern lernen Mathe über Studimup. 8 Schüler, die über Studimup lernen, schreiben eine 1 im Mathe Test, insgesamt gibt es 10 Einser. Wie hoch ist die Wahrscheinlichkeit, dass wenn man über Studimup gelernt hat, man eine 1 schreibt? | Einblenden | |
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
