Äquivalenzumformung
Die Äquivalenzumformung ist wichtig, um Gleichungen lösen zu können. Sie ist dafür da, um bei einer Gleichung die Unbekannte auf einer Seite zu isolieren (also nach einer Variablen aufzulösen), sodass man die Unbekannte bestimmen kann. Es soll also am Ende dastehen x=... . Das funktioniert, indem man einen Äquivalenzstrich hinter der Gleichung macht, welcher aussagt, dass die Rechenoperation, welche dahintersteht, auf beiden Seiten der Gleichung durchgeführt wird. Das darf man, weil wenn etwas auf beiden Seiten multipliziert, addiert, subtrahiert, ... wird, sich der Wert der Gleichung nicht verändert, so, wie wenn man dasselbe Gewicht auf beide Enden einer Waage legt.
Addition und Subtraktion
Wollt ihr etwas mit Plus oder Minus auf die andere Seite bringen, schreibt ihr das hinter dem Äquivalenzstrich hin und führt diese Aktion dann auf beiden Seiten durch. Führt diese Operation immer mit dem gegenteiligen Rechenzeichen durch, so fällt es auf der einen Seite weg und ist dann auf der anderen Seite.
Beispiele:
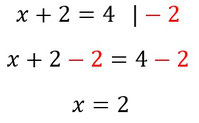

Aufgaben mit Lösungen:
Klick auf einblenden, um die Lösung zu sehen.
Mulitplikation und Division
Wollt ihr etwas mit mal oder geteilt auf die andere Seite bringen, schreibt ihr das hinter den Äquivalenzstrich und führt das auf beiden Seiten durch. Es ist wichtig, dass ihr JEDEN Summanden auf beiden Seiten multiplizieren oder teilen müsst (siehe "Rechenregel" weiter unten).
Beispiele:
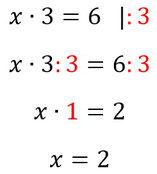
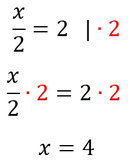
Aufgaben mit Lösungen:
Klick auf einblenden, um die Lösung zu sehen.
Potenzieren und Wurzel-ziehen
Wenn ihr eine Potenz/Wurzel habt, dann könnt ihr diese mit einer Wurzel/Potenz auflösen. Dabei ist der Wurzelexponent immer dem Exponenten der Potenz gleich. Wird also zum Beispiel etwas quadriert, kann dies mit der 2. Wurzel (die „gewöhnliche“ Wurzel) auf die andere Seite „gebracht“ werden.
Beispiele:

und
x = -2

Aufgaben mit Lösungen:
Klickt auf einblenden, um die Lösung zu sehen.
Mischung aus mehreren Rechenoperationen
Habt ihr eine Mischung aus mehreren Rechenoperationen, müsst ihr diese hintereinander durchführen. Wichtig ist, dass ihr in der richtigen Reihenfolge umformt, damit es nicht zu kompliziert wird, also:
- Addition und Subtraktion
- Multiplizieren und Dividieren
- Wurzel ziehen und Potenzieren
Hier ein Beispiel dafür:
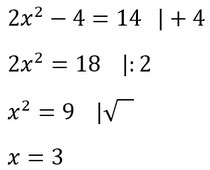
Aufgaben mit Beispielen:
Klick auf einblenden, um die Lösungen zu sehen.
| 3x-2=4 | Einblenden | |
|
Lösung: 3x-2=4 |+2 3x=6 |:3 x=2 |
||
| 2(x)^2+2=10 | Einblenden | |
|
Lösung: 1. Strichrechnung umformen 2(x)^2+2=10 |-2 2. Punktrechnung umformen 2(x)^2=8 |:2 3. Wurzel oder Exponent umfromen x^2=4 |√ x=2 |
||
| 5x+2=7 | Einblenden | |
|
Lösung: 5x+2=7 |-2 5x=5 |:5 x=1 |
||
| 2√(x)+2=10 | Einblenden | |
|
Lösung: 2√(x)+2=10 |-2 2√(x)=8 |:2 √x=4 |( )^2 x=16 |
||
Rechenregel
Ihr müsst folgende Regel bei der Äquivalenzumformung beachten:
Wird nach dem Äquivalenzstrich multipliziert, dividiert, die Wurzel gezogen oder potenziert, müsst ihr dies immer für die „ganze Seite“ einer Gleichung durchführen.
Dafür setzt ihr Klammern um den ganzen Term nach/vor dem „=“ und schreibt da die Rechenoperation dran.

Und NICHT:

Ungleichungen richtig umfromen und lösen
Ihr könnt diese Gleichungen ganz normal mit der Äquivalenzumformung umformen, ihr müsst nur eine Kleinigkeit beachten, und zwar, dass sich das größer und kleiner Zeichen bei bestimmten Umformungen umdreht, nämlich wenn man... :
- ... die Gleichung mit einer negativen Zahl multipliziert
- ... die Gleichung mit einer negativen Zahl dividiert
- ... die Gleichung mit einer negativen Zahl potenziert (hoch -1 z.B.)
- ... auf beiden Seiten der Gleichung den Kehrbruch bildet
Beispiele:
-2x < 4 |:(-2)
x > -2
-0,2x > 1 | ·(-5)
x < -5
5x ≤ 10 |:5
x ≤ 2
6x+2 ≥ 8 |-2
6x ≥ 6 |:6
x ≥ 1
