Quadratische Ergänzung
Die quadratische Ergänzung ist dafür da, eine Gleichung mit einem quadratischen Bestandteil umzuformen. Beispielsweise, wenn man eine quadratische Gleichung von der gewöhnlichen, in die Scheitelpunktform umformen möchte.
Quadratische Ergänzung Schritt für Schritt richtig durchführen:
- Klammert die Zahl vor dem x2 von x2 und x aus
- Bestimmt die Hälfte der Zahl vor dem x
- Quadriert sie
- Addiert die Zahl in die Klammer hinten dran und subtrahiert sie gleich wieder
- Wendet die binomische Formel in der Klammer an
- Multipliziert die Klammer wieder aus
Schritt für Schritt Vorgehen der quadratischen Ergänzung

Ihr möchtet beispielsweise diese Gleichung quadratisch ergänzen, um die Scheitelpunktform zu erhalten:

Klammert erst die 2, also die Zahl vor dem x2, von x2 und x aus.
Dazu lässt ihr die Zahl vor dem x2 weg und teilt die Zahl vor dem x durch 2. Wie man richtig ausklammert, könnt ihr unter Ausklammern nochmal durchlesen.

Das Ergebnis sieht dann so aus.

Nun addiert und subtrahiert ihr die quadrierte Hälfte von der Zahl vor dem x (die Hälfte von 2 ist 1).

Wie ihr seht, habt ihr dann einen Teil, den ihr mit der binomischen Formel umwandeln könnt, also macht dies dann auch.
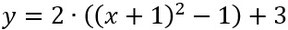
Wenn ihr dies gemacht habt, sieht es dann so aus.

Nun müsst ihr die große Klammer nur noch auflösen, indem ihr ausmultipliziert. Dazu multipliziert ihr die Zahl vor der Klammer mit den beiden Teilen drinnen, also der binomischen Formel und der einen quadrierten Zahl, die ihr noch habt.

Das Ergebnis sieht dann so aus. Nun könnt ihr die hinteren beiden Zahlen nur noch addieren und ihr seid fertig.
Aufgaben zur quadratischen Ergänzung
Hier par Aufgaben zur quadratischen Ergänzung. Klickt auf einblenden, um eine Lösung mit Zwischenschritten zu erhalten.
| y=3x2+6x+3 | Einblenden | |
|
Lösung:
|
||
| y=4x2+4x+4 | Einblenden | |
|
Lösung:
|
||
| y=2x2+8x+5 | Einblenden | |
|
Lösung:
|
||
| y=6x2+3x+4 | Einblenden | |
|
Lösung:
|
||
Weitere Aufgaben
Aufgaben zu diesem Thema findet ihr über den Button. Dort könnt ihr euch Übungsblätter downloaden oder die Aufgaben einfach von dort abschreiben. Lösungen zu den Aufgaben findet ihr dort ebenfalls:
