Gleichungssysteme lösen
Gleichungssysteme sind mehrere Gleichungen mit mehreren Variablen bzw. Unbekannten. Um Gleichungssysteme lösen zu können, sind immer mindestens genauso viele Gleichungen wie Unbekannte nötig. Es gibt hierfür drei mögliche Lösungsverfahren:
Additionsverfahren
Beim Additionsverfahren wird eine Variable durch Addition oder Subtraktion eliminiert, wodurch nur noch eine übrig bleibt. Schritt für Schritt geht ihr so vor:
- Guckt, welche der Gleichungen ihr mit einer Zahl multiplizieren müsst, sodass der Faktor vor einer Variablen in beiden Gleichungen gleich ist.
- Danach addiert oder subtrahiert ihr beide Gleichungen miteinander/voneinander, sodass eine Variable wegfällt.
- Danach löst ihr die Gleichung nach der verbleibenden Variablen auf, so habt ihr für diese schon die Lösung.
- Setzt in eine der beiden Gleichungen vom Beginn die Variable ein, die ihr im vorherigen Schritt berechnet habt, und löst nach der verbleibenden auf.
Beispiel: Additionsverfahren Schritt für Schritt
- Gegeben sind diese beiden Gleichungen.
- Nehmt die I. Gleichung mal 2, sodass in beiden Gleichungen derselbe Faktor vor dem y steht (die 4). Übrigens ist es egal welchen Faktor vor einer Variable ihr gleich macht, sucht euch das einfachste raus.
- Nehmt die II. Gleichung minus die I., sodass y wegfällt. Löst dann nach x auf (hier nicht mehr nötig, da x bereits alleine auf einer Seite ist).
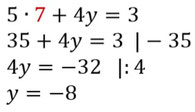
- Setzt nun das Ergebnis, welches ihr für x erhalten habt, in eine der beiden Gleichungen vom Beginn ein, dann könnt ihr leicht y ausrechnen. Dann seid ihr schon fertig.
Das Ergebnis für dieses Gleichungssystem sind dann: x=2 und y=3.
Aufgaben zum Additionsverfahren
Hier sind Aufgaben zum Üben des Additionsverfahrens mit Lösungen:
Einsetzverfahren
Beim Einsetzverfahren eliminiert ihr eine Variable durch Einsetzen:
- Löst eine der Gleichungen nach einer Variablen auf (egal ob x oder y). Tipp: Am besten löst ihr nach einer Variablen auf, welche keinen Vorfaktor hat (oder eine 1 als Vorfaktor).
- Setzt das Ergebnis für die Variable, nach der ihr aufgelöst habt, in die 2. Gleichung ein.
- Jetzt habt ihr eine Variable weniger und könnt nach der anderen auflösen. So erhaltet ihr den Wert für diese Variable.
- Setzt den Wert dieser Variable, welchen ihr jetzt kennt, in eine der beiden Gleichungen vom Anfang ein und löst nach der anderen Variable auf. So erhaltet ihr auch den Wert für diese.
Beispiel: Einsetzverfahren Schritt für Schritt
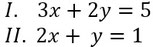
- Es sind diese Zwei Gleichungen gegeben.
- Löst eine der Gleichungen nach einer Variablen auf. Hier wird Gleichung II. nach y aufgelöst.
- Setzt dieses Ergebnis in die andere Gleichung (hier in Gleichung I.) für die Unbekannte ein, also für y (1-2x) einsetzen. Vorsicht Klammern nicht vergessen!
- Formt dieses Ergebnis nach x um. Jetzt wisst ihr die Lösung für x.
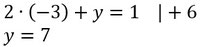
- Setzt x in eine der beiden Gleichungen vom Anfang ein und löst nach y auf, so erhaltet ihr den Wert für y. Hier wurde y in die I. Gleichung eingesetzt.
Das Ergebnis für dieses Gleichungssystem ist dann: x=-3 und y=7
Aufgaben zum Einsetzverfahren
Hier sind Aufgaben, mit denen ihr euer Können im Einsetzverfahren testen könnt:
Gleichsetzverfahren
Beim Gleichsetzverfahren eliminiert ihr eine Variable durch Gleichsetzen:
- Löst 2 Gleichungen nach derselben Variablen auf
- Setzt die Gleichungen gleich, also die eine = die Andere.
- Löst nach der verbleibenden Variablen auf, so erhaltet ihr ihren Wert.
- Setzt den Wert der Variablen, welche ihr jetzt schon kennt, in eine der beiden Gleichungen vom Anfang ein und ihr habt auch die Lösung für die 2. Variable.
Beispiel zum Gleichsetzverfahren
- Ihr habt diese beiden Gleichungen gegeben.
- Da beide Gleichungen bereits nach derselben Variablen aufgelöst sind, kann man direkt gleichsetzten. Also setzt beide Gleichungen rechts von y gleich.
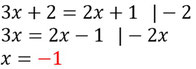
- Löst jetzt nach x auf.
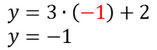
- Setzt den Wert für x in eine der beiden Gleichungen von oben ein, um y zu erhalten.
Die Lösung für dieses Gleichungssystem ist also: x=-1 und y=-1
Aufgaben zum Gleichsetzverfahren
Testet euer Wissen im Gleichsetzverfahren mit folgenden Aufgaben. Die Lösung könnt ihr mit "Einblenden" öffnen.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
