Gleichungen lösen und umformen
Hier eine Übersicht, wie ihr vorgehen müsst, um verschiedene Arten von Gleichungen zu lösen oder umzuformen:
Lineare Gleichungen
Um lineare Gleichungen zu lösen oder umzuformen, müsst ihr die Gleichung mit der Äquivalenzumformung so umstellen, dass das x alleine auf der einen Seite vom „=“ steht und der Rest auf der anderen.
Beispiele:


Aufgaben zum Üben vom Lösen linearer Gleichungen:
Quadratische Gleichungen
Bei quadratischen Gleichungen müsst ihr die Gleichung so mit der Äquivalenzumformung umformen, dass auf der einen Seite vom „=“ die 0 steht. Danach könnt ihr die Mitternachtsformel anwenden und ihr erhaltet die Lösung(en).
Beispiele:

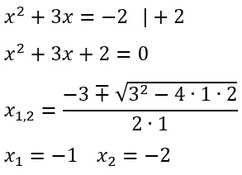
Aufgaben zum Üben vom Lösen quadratischer Gleichungen:
| 3x2+5x=8 | Einblenden | |
|
Lösung 3x2+5x=8 |-8 3x2+5x-8=0 In die Mitternachtsformel einsetzen: 1. x=1 2. x=-8/3 |
||
| x2+2x=8 | Einblenden | |
|
Lösung x2+2x=8 |-8 x2+2x-8=0 In die Mitternachtsformel einsetzen: 1. x=2 2. x=-4 |
||
Wurzelgleichung
Wurzelgleichungen kann man lösen oder umformen, indem man alles bis auf die Wurzel mit der Unbekannten auf eine Seite vom „=“ bringt und den Rest auf die Andere. Danach muss man nur noch potenzieren (quadrieren) und man erhält die Lösung.
Beispiele:


Aufgaben zum Üben vom Lösen von Wurzelgleichungen:
Potenzgleichung
Potenzgleichungen funktionieren fast genauso wie die Wurzelgleichungen, man bringt alles bis auf die Potenz auf eine Seite und den Rest auf die Andere. Danach zieht man nur noch die Wurzel und erhält das Ergebnis.
Beispiele:


Aufgaben zum Üben des Lösens von Potenzgleichungen:
| x2=9 | Einblenden | |
|
Lösung: x2=9 |√ x=3 |
||
| 5x2+2=127 | Einblenden | |
|
Lösung 5x2+2=127 |-2 5x2=125 |:5 x2=25 |√ x=5 |
||
Exponentialgleichung
Um eine Exponentialgleichung zu lösen, formt ihr die Gleichung zunächst so um, sodass der Exponentialteil alleine auf der einen Seite steht. Dann führt ihr den Logarithmus auf beiden Seiten durch, wodurch ihr die Lösung erhaltet.
Beispiele:


Aufgaben zum Üben vom Lösen von Exponentialgleichungen:
| 2x+2=10 | Einblenden | |
|
Lösung 2x+2=10 |-2 2x=8 |lg x·lg2=lg8 |:lg2 x=3 |
||
| 3x+4=13 | Einblenden | |
|
Lösung 3x+4=13 |-4 3x=9 |lg x·lg3=lg9 |:lg3 x=2 |
||
Logarithmusgleichung
Um eine Logarithmusgleichung zu lösen oder umzuformen, formt ihr die Gleichung so um, dass der Logarithmus auf einer Seite steht und formt ihn mithilfe der Definition des Logarithmus um, wodurch ihr die Lösung erhaltet.
Beispiele:


Aufgaben zum Üben vom Lösen von Logarithmusgleichungen:
Weitere Aufgaben zum Üben
Aufgaben zu diesem Thema findet ihr über den Button unten. Dort könnt ihr euch diese downloaden. Lösungen zu den Aufgaben findet ihr dort ebenfalls:
