Brüche und Bruchrechenregeln
Übersicht: klickt auf das, was ihr wissen möchtet und es bewegt sich automatisch zu der Stelle wo dies steht:
Was ist ein Bruch?
Ein Bruch besteht aus einem Zähler und Nenner, dabei wird der Zähler durch den Nenner geteilt, daher ist es einfach eine andere Schreibweise für eine Division. Diese hat dann den Vorteil, dass sie leichter zu schreiben ist und man keine Kommazahlen benötigt, falls die beiden Zahlen nicht restlos teilbar sind.

Vorstellung eines Bruchs
Ihr könnt euch Brüche mit Tortenstücken vorstellen, dabei ist der Nenner (die Zahl unten) die Anzahl, in die eine ganze Torte geteilt wurde. Der Nenner ist dann die Anzahl an Stücken.

Zähler und Nenner
- Zähler ist die Zahl, die oben im Bruch steht
- Nenner ist die Zahl, die unten im Bruch steht

Mit der Vorstellung von davor, ist die untere Zahl sozusagen die Anzahl, in wie viele Stücke die Torte geschnitten wurde und die obere Zahl, die Anzahl an Stücken die man haben möchte.
Nenner darf nie Null sein
Eine der wichtigsten Bruchrechenregeln ist, dass der Nenner nicht 0 sein darf! Man darf schließlich nicht durch 0 teilen. Das ist wichtig und ist auch manchmal nützlich, wenn ihr mal Definitionslücken von Funktionen bestimmen müsst. ;)
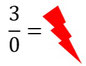
Gemischte Brüche
Gemischte Brüche sind Brüche, welche nicht nur aus einem Bruch bestehen, sondern auch aus einer ganzen Zahl. Diese Brüche dienen der Veranschaulichung. Ihr könnt gemischte Brüche in unechte Brüche (siehe weiter unten) umwandeln und umgekehrt.
Bedeutung: Die Zahl vor dem Bruch gibt an, wie viele ganze Teile angegeben werden und der Bruch dahinter den nicht ganzen Anteil.
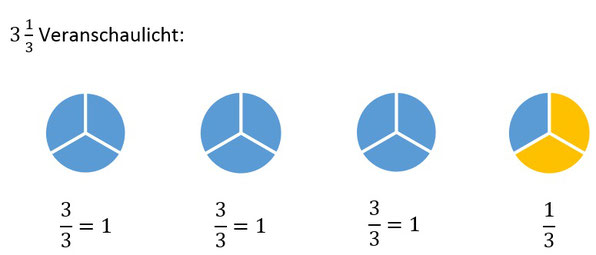
Also 3 ganze "Kuchen" und ein Drittel.
Gemischte Brüche umwandeln
Wenn ihr gemischte Brüche umwandeln möchtet, geht ihr so vor:
- Multipliziert die Zahl vor dem Bruch mit dem Nenner
- Addiert das Ergebnis zum Zähler
Beispiel:

Zahl mal Nenner: 4·3 = 12

Addiert das Ergebnis zum Zähler.
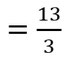
Das ist nun der unechte Bruch.
Beispiele zum Umwandeln gemischter Brüche

Echte und unechte Brüche
Unechte Brüche sind alle Brüche, bei denen der Nenner kleiner oder gleich dem Zähler ist. Echte Brüche sind alle, bei denen der Zähler kleiner ist als der Nenner.


Kehrwert
Der Kehrwert eines Bruchs ist leicht zu bilden, man vertauscht einfach Zähler und Nenner, dann ist man schon fertig :)

Erweitern
Erweitern ist das Gegenteil von Kürzen. Es wird also eine Zahl mal Nenner und Zähler genommen, sodass dort größere Werte stehen. Der Wert des Bruchs ändert sich dabei jedoch nicht. Dabei muss im Nenner und Zähler mit derselben Zahl multipliziert werden!

Beispiele:

Kürzen
Das Kürzen hat von nun an eine eigene Seite :) Wir haben dieses Kapitel nun mit mehr Beispielen und ausführlicher erklärt.
Arbeitsblätter zu Brüchen
Aufgaben zu diesen Themen findet ihr über die Buttons unten. Dort könnt ihr euch diese kostenlos und inklusive Lösungen downloaden.
