Lage von Geraden und Ebenen

Für die Lage einer Geraden zu einer Ebene gibt es 3 Möglichkeiten:

• Die Gerade liegt in der Ebene drinnen
• Die Gerade ist parallel zur Ebene
• Die Gerade schneidet die Ebene

Möchtet ihr die Lage einer Geraden zu einer Ebene bestimmen, geht ihr Schritt für Schritt so vor:

1. Stellt sicher, dass die Ebene in Koordinatenform ist und die Gerade in Parameterform, wenn nicht müsst ihr diese noch umformen. Wie das geht, findet ihr im Artikel zum Umformen von Ebenengleichungen.
2. Setzt die Geradengleichung in die Ebenengleichung ein (dabei ist die erste Zeile der Geradengleichung x1, die zweite Zeile x2, die 3. Zeile x3. (Im Beispiel könnt ihr euch dies noch genauer anschauen)
3. Löst diese Gleichung und dann gibt es 3 Möglichkeiten, was ihr erhaltet:
   1. Die Gleichung ist für alle λ erfüllt, dass bedeutet ihr erhaltet ein Ergebnis, das wahr ist egal für welches λ. Z.B. 1=1 oder 2=2. In diesem Fall liegt die Gerade in der Ebene.
   2. Die Gleichung ist für kein λ erfüllt, dass bedeutet ihr erhaltet ein Ergebnis, das falsch ist egal für welches λ. Z.B. 2=5 oder 4=1. In diesem Fall ist die Gerade parallel zur Ebene.
   3. Die Gleichung ist für genau ein λ erfüllt, dass bedeutet ihr erhaltet ein Ergebnis, das dem λ einen Wert zuweist. Z.B. λ=1 oder λ=-3. In diesem Fall hat die Gerade an diesem Wert für λ einen Schnittpunkt. Um diesen dann zu berechnen, setzt ihr einfach dieses λ in die Gleichung ein und berechnet den Punkt dafür. Das ist dann euer Schnittpunkt.

Seien diese Gerade und Ebene gegeben:

Bestimmt zunächst die drei x Werte, dies sind einfach die Zeilen der Geradengleichung einzeln aufgeschrieben von oben nach unten:

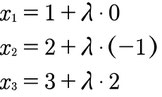
Setzt diese Werte einfach in die Ebenengleichung ein, also x1 für x1 usw. und löst die Gleichung, die ihr so erhaltet:

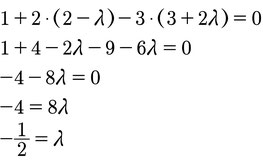
Wie gesagt kommt da eine Gleichung raus, die wahr ist für alle λ (z.B. 1=1), dann liegt die Gerade in der Ebene, kommt eine Gleichung raus die für kein λ wahr ist (z.B. 2=1), dann ist die Gerade parallel und kommt wie hier eine Gleichung raus, bei der ihr einen bestimmten Wert für λ erhaltet, schneidet die Gerade die Ebene an dieser Stelle, setzt also das λ in die Geradengleichung ein und ihr erhaltet so den Schnittpunkt:

Hier könnt ihr euch die Lage der Geraden und der Ebene mal in 3D angucken:

• Gleichungssysteme lösen
• Koordinatenform und Normalenform einer Ebene
• Parameterform
• Lagebeziehungen von Geraden
• Lage Ebene und Ebene bestimmen
• Ebenengleichungen umformen
• Abstand Punkt und Punkt
• Abstand Punkt und Gerade
• Abstand Gerade und Gerade
• Abstand Punkt und Ebene

In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.