Abstand von Ebene und Punkt berechnen

Möchtet ihr den Abstand eines Punktes zu einer Ebene berechnen, auch Lotfußpunktverfahren genannt, geht ihr so vor:

  1. Ihr formt, falls noch nicht der Fall, die Ebenengleichung in die Koordinatenform um. Hier findet ihr noch mal alle Umformungen:
  2. Bestimmt den Normalenvektor aus der Koordinatenform (das was vor dem x1 steht, ist ganz oben im Vektor, das was vor dem x2 steht darunter und das was vor dem x3 steht ganz unten, sollte eins von den x-en nicht da sein schreibt ihr 0 dafür hin)
  3. Teilt die Koordinatenform durch den Betrag des Normalenvektors, bzw. nimmt sie mal den Kehrbruch des Normalenvektors, so erhaltet ihr die Hessesche Normalform
  4. Setzt den Punkt in die hessesche Normalform ein, also das, was ganz oben vom Vektor des Punktes für x1 steht, das darunter für x2 und das ganz unten für x3.
  5. Das, was raus kommt, ist euer Abstand. Sollte der Wert negativ sein, nehmt den Betrag davon, denn ein Abstand kann ja schließlich nicht negativ sein.

Beispiel: Abstand zwischen Ebene und Punkt berechnen

Sei folgende Ebene und Punkt gegeben:

 

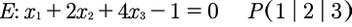
Beispiel einer Ebenengleichung und eines Punkts
  • Bestimmt zunächst den Normalenvektor, dies könnt ihr in der Koordinatenform durch Ablesen der Faktoren die vor den x-Werten stehen (das vor dem x1 steht ganz oben, das vor dem x3 ganz unten):
Beispiel für einen Normalenvektor
  • und berechnet davon den Betrag:
Beispiel zur Berechnung des Betrags eines Vektors
  • Dann teilt ihr die Koordinatenform durch den Betrag des Normalenvektors, bzw. nehmt sie mal den Kehrbruch des Normalenvektors, das nennt man dann hessesche Normalenform:
Hessesche Normalenform einer Ebene
  • Danach setzt ihr nur noch den Punkt ein und berechnet das Ergebnis (setzt für x1 das ein, was im Vektor ganz oben steht und für x3 das, was ganz unten steht). Sollte das Ergebnis negativ sein, nehmt den Betrag davon. Das ist dann euer Abstand:
Berechnung des Abstands zwischen einer Ebene und einem Punkt

Passende Themen