Umkehrfunktion von Funktionen
Erklärung: Eine Umkehrfunktion ist die Umkehrung einer Funktion. Es geht also einfach ausgedrückt darum herauszufinden, welches x man einsetzen musste, um ein bestimmtes y zu erhalten. Also der umgekehrte Weg einer Funktion und daher Umkehrfunktion. Meist nennt man die Umkehrfunktion dann f-1.
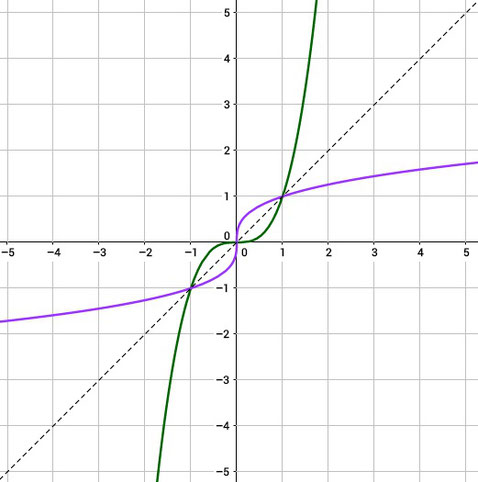
Hier seht ihr die Funktion f(x)=x3, welche grün eingezeichnet ist und ihre Umkehrfunktion f-1(x)=x1/3, welche lila eingezeichnet ist. Wie ihr vielleicht seht, entspricht die Umkehrfunktion einer Spiegelung an einer Achse, welche 45° zur x-Achse steht, bzw. die Gleichung y=x hat.
Umkehrfunktion bestimmen
Um die Umkehrfunktion zu bestimmen, geht ihr so vor:
- Zunächst löst man die Funktion nach x auf, also die Funktion so umformen, dass da steht: x=....
- Danach vertauscht man nur noch das x und das y miteinander und fertig, man hat die Umkehrfunktion.
Beispiel:
Gegeben ist die Funktion:
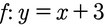
- formt erst nach x um:
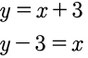
- Danach vertauscht ihr nur noch x und y und ihr habt die Umkehrfunktion:
Aufgaben (mit Lösungen):
Hier sind par Aufgaben mit Lösungen, die könnt ihr euch angucken oder als Übung lösen. Klickt auf Einblenden, um die Lösung zu sehen:
| Was ist die Umkehrfunktion von f(x)=x+2? | Einblenden | |
| Was ist die Umkehrfunktion von f(x)=x3+8? | Einblenden | |
Definitions- und Wertemenge
Die Umkehrfunktion vertauscht auch die Definitions- und Wertemenge einer Funktion. Das bedeutet, dass die Definitionsmenge der ursprünglichen Funktion, die Wertemenge der Umkehrfunktion ist und die Wertemenge der ursprünglichen Funktion, die Definitionsmege der Umkehrfunktion.
Wann gibt es eine Umkehrfunktion?
Eine Funktion hat nur eine Umkehrfunktion, wenn jeder y-Wert höchstens einmal "getroffen wird", also wenn man einen y-Wert nur für ein bestimmtes x erhält. Mathematisch ausgedrückt: Ist die Definitionsmenge größer als die Wertemenge gibt, es keine Umkehrfunktion.
Zum Beispiel kommen bei der Funktion y=x2 für x=-2 und x=2 derselbe y-Wert mit verschiedenen x-Werten raus und daher hat sie keine Umkehrfunktion. Die Definitionsmenge ist hier größer als die Wertemenge, da in der Definitionsmenge alle reellen Zahlen sind, jedoch in der Wertemenge nur die positiven reellen Zahlen und die Null.
Man kann aber das Problem umgehen, indem man die Definitionsmenge so verändert, dass das nicht mehr passiert und die Funktion trotzdem eine Umkehrfunktion hat, dazu wählt ihr die Definitionsmenge so, dass jeder y-Wert höchstens einmal getroffen wird, bzw. dass die Definitionsmenge nichtmehr größer ist als die Wertemenge.
Bei der Funktion y=x2 wäre es möglich die Definitionsmenge nur mit positiven Zahlen anzugeben, dann hätte sie eine Umkehrfunktion, nämlich die Wurzelfunktion. Wenn man nur positive Zahlen einsetzen darf, kann derselbe y-Wert nicht mehr bei zwei verschiedenen xWerten rauskommen.
Zusammengefasst hat eine Funktion KEINE Umkehrfrunktion, wenn...:
- ...entweder die Definitionsmenge mehr Elemente hat als die Wertemenge...
- ...oder wenn für zwei verschiedene x derselbe y-Wert raus kommt....
- ...oder wenn die Funktion mehr als eine Nullstelle hat.
Jedoch kann man die Definitionsmenge dann anders Wählen, sodass man trotzdem eine Umkehrfunktion angeben kann.
Passende Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
