Symmetrie von Funktionen bestimmen

Zum Thema Symmetrie bei Figuren geht´s hier. Es gibt bei Funktionen 2 wesentliche Arten von Symmetrie die ihr kennen müsst:

Achsensymmetrie von Funktionen

Die Achsensymmetrie liegt vor, wenn die Funktion eine senkrechte Spiegelachse hat. 

  • diese liegt vor, wenn f(-x)=f(x) ist
  • diese Symmetrie kommt fast ausschließlich bei Funktionen mit geradem Exponenten und der Betragsfunktion vor.

Hier seht ihr ein Beispiel für Achsensymmetrie. Das Rote ist die Symmetrieachse, was hier gleichzeitig die y-Achse ist.

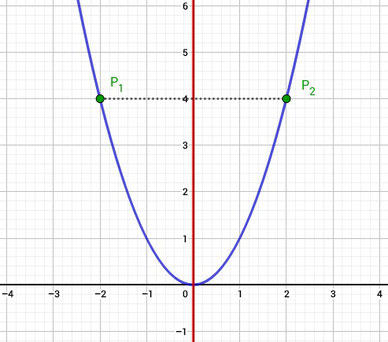
Achsensymmetrie einer Funktion grafisch veranschaulicht

Schritt für Schritt Anleitung zur Bestimmung der Achsensymmetrie

Punktsymmetrie von Funktionen

Punktsymmetrie bedeutet, dass die Funktion einen Spiegelpunkt hat. An diesem Spiegeln sich alle Werte der Funktion.

  • Punktsymmetrie liegt vor, wenn -f(x)=f(-x) ist
  • Diese Symmetrie kommt unter anderem bei Funktionen mit ungeraden Exponenten vor

Hier ein Beispiel für Punktsymmetrie, dabei ist der Koordinatenursprung der Spiegelpunkt.

Punktsymmetrie einer Funktion grafisch veranschaulicht

Schritt für Schritt Anleitung zur Bestimmung der Punktsymmetrie

Auf Achsensymmetrie überprüfen

Symmetrisch zur y-Achse?

Möchtet ihr wissen, ob eine Funktion achsensymmetrisch zur y-Achse ist, geht ihr so vor: 

Prüft, ob für f(-x)=f(x) dasselbe rauskommt, also setzt einmal -x in die Funktion ein und schaut, ob dasselbe rauskommt wie bei +x, wenn ja ist sie achsensymmetrisch.  

 

Beispiel:

  • Ist diese Funktion achsensymmetrisch? 
Beispiel einer achsensymmetrischen Funktion

  • Kommt für f(-x) dasselbe für f(x) raus? Also setzt statt x, -x in die Funktion ein. 
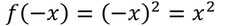
Beispiel zur Überprüfung einer Funktion auf Achsensymmetrie zur y-Achse

  • Wie ihr seht, kommt für f(-x) dasselbe raus, wie für f(x). Also ist die Funktion achsensymmetrisch zur y-Achse.
Lösung des Beispiels zur Achsensymmetrie

Verschobene Funktion achsensymmetrisch?

Ist die Funktion nach links oder rechts verschoben (siehe Artikel zur Verschiebung), müsst ihr die Funktion ohne Verschiebung auf Achsensymmetrie untersuchen. Ist sie dann achsensymmetrisch, ist die verschobene Funktion ebenfalls achsensymmetrisch und die Spiegelachse ist um denselben Wert verschoben wie die Funktion. 

 

Beispiel:

  • Ist diese Funktion achsensymmetrisch?
Beispiel für eine achsensymmetrische Funktion

  • Wie ihr merkt, ist die Funktion um zwei nach rechts verschoben. Also müsst ihr sie erstmal ohne Verschiebung betrachten (lasst also die Zahl am x weg).
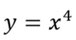
Funktion ohne Verschiebungen

  • Überprüft nun die Funktion ohne Verschiebung auf Achsensymmetrie. Es kommt für -x und +x dasselbe raus, also ist die Funktion achsensymmetrisch.
Überprüfung der Funktion auf Achsensymmetrie

  • Wie ihr seht, ist die Funktion achsensymmetrisch. Da sie aber um 2 nach rechts verschoben ist, ist auch die Symmetrieachse um 2 nach rechts verschoben.
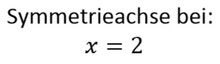
Lösung durch Angabe der Symmetrieachse

Die Funktion und Symmetrieachse sehen dann so aus:

Grafische Darstellung der Funktion mit Symmetrieachse

Achsensymmetrisch zu bestimmter Achse?

Möchtet ihr wissen, ob eine Funktion zu einer bestimmten Achse symmetrisch ist, geht ihr so vor: 

1. Setzt für x in die Funktion x0+h ein, dabei ist x0 die x-Koordinate bei der die mögliche Symmetrieachse liegt. Mathematisch sieht das so aus: 

Allgemeine Form zur Überprüfung einer Funktion auf Achsensymmetrie

2. Macht das ganze nochmal, nur mit einem Minus, also:

Zweiter Teil der allgemeinen Formel zur Überprüfung der Achsensymmetrie

3. Vereinfacht beides soweit wie möglich.

4. Kommt bei beidem dasselbe raus, dann ist diese Achse die Symmetrieachse der Funktion

 

 

Beispiel:

Ist die Funktion f(x) = x2-4x+4 achsensymmetrisch zu der Achse x = 2? 

  • Setzt nun für jedes x, wie oben beschrieben, 2+h ein (2 ist x0, also die Stelle bei der die Achse liegt): 
Beispiel zur Überprüfung einer Funktion auf Achsensymmetrie
  • Vereinfacht das soweit wie möglich:
Rechenschritte zur Bestimmung der Symmetrie einer Funktion
  • Setzt jetzt in die Funktion 2-h ein:
Beispiel des zweiten Teils der Überprüfung auf Achsensymmetrie
  • Vereinfacht auch das soweit wie möglich: 
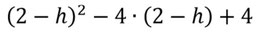
Beispiel der Rechenschritte
Lösung der Überprüfung auf Achsensymmetrie

Vergleicht beide Ergebnisse. Hier kommt beide Male h2 raus, also sind die Ergebnisse gleich. Somit ist x=2 die Symmetrieachse dieser Funktion.

Grafische Darstellung einer achsensymmetrischen Funktion

Aufgaben zur Achsensymmetrie von Funktionen

Ist die Funktion f(x)=x4 achsensymmetrisch? Einblenden
Ist die Funktion f(x)=(x+2)2+1 achsensymmetrisch? Einblenden
Arbeitsblätter zur Symmetrie von Funktionen

Auf Punktsymmetrie überprüfen

Symmetrisch zum Ursprung?

Möchtet ihr wissen, ob eine Funktion punktsymmetrisch zum Ursprung ist, geht ihr so vor: 

Punktsymmetrie liegt vor, wenn -f(x)=f(-x), also nehmt einmal die ganze Funktion mal -1 und einmal nur -x für x einsetzen, wenn beide Male dasselbe rauskommt, ist sie punktsymmetrisch zum Ursprung. 

 

Beispiel:

  • Ist diese Funktion punktsymmetrisch?
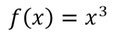
Beispiel einer punktsymmetrischen Funktion zum Ursprung

  • Nehmt einmal die Funktion mal -1 und einmal setzt ihr für x, -x ein. Wie ihr seht, kommt beide male dasselbe raus, also ist die Funktion punktsymmetrisch.
Rechenweg zur Überprüfung einer Funktion auf Punktsymmetrie zum Ursprung

Verschobene Funktion punktsymmetrisch?

Ist eine punktsymmetrische Funktion verschoben, müsst ihr aufpassen, dann müsst ihr nur die reine Funktion ohne Verschiebungen so überprüfen (also lasst die Verschiebung in y-Richtung und x-Richtung weg). Die Verschiebungen sind dann der Symmetriepunkt (also ist es eine punktsymmetrische Funktion, aber z.B. 3 nach oben und eins nach links verschoben, dann ist der Symmetriepunkt (1|3)).

 

Beispiel:

  • Ist diese Funktion punktsymmetrisch? 
Beispiel für eine verschobene punktsymmetrische Funktion

  • Da diese Funktion verschoben ist, müsst ihr sie erstmal ohne Verschiebungen betrachten. Vom Beispiel weiter oben wisst ihr bereits, dass sie punktsymmetrisch ist.
Funktion ohne Verschiebungen

  • Da die Funktion um 2 nach rechts und 1 nach oben verschoben ist, ist der Spiegelpunkt genau an dieser Stelle.
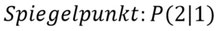
Angabe des Spiegelpunkts dieser Funktion

Punktsymmetrisch zu bestimmtem Punkt?

Möchtet ihr eine Funktion auf Punktsymmetrie zu einem bestimmten Punkt überprüfen, macht ihr das so: 

 

1.Setzt den Punkt, welcher der Symmetriepunkt sein soll, für x0 und y0 so in die Funktion ein:

Erster Teil der Formel zur Überprüfung, ob eine Funktion zu einem bestimmten Punkt punktsymmetrisch ist.

(also setzt für x die x-Koordinate des Punktes in die Funktion ein plus h, dann zieht ihr von der Funktion die y-Koordinate des vermutlichen Symmetriepunktes ab, siehe Beispiel).

2. Setzt den Punkt, welcher der Symmetriepunkt sein soll, für x0 und y0 jetzt so in die Funktion ein: 

Zweiter Teil der Formel zur Überprüfung, ob eine Funktion punktsymmetrisch zu einem bestimmten Punkt ist

3. Vereinfacht beides soweit wie möglich. Kommt bei beiden dasselbe raus, dann ist der Punkt der Symmetriepunkt.

 

 

Beispiel:

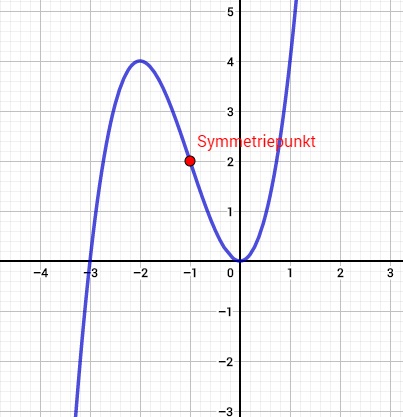
Ist diese Funktion punktsymmetrisch zum Punkt (-1|2):

Beispiel für eine Funktion, welche zu einem bestimmten Punkt punktsymmetrisch ist
  • Setzt alles in die Formel von oben ein, also für x setzt ihr (-1+h) ein (-1 ist die x-Koordinate vom Punkt). Am Ende zieht ihr dann 2 ab (yKoordinate vom Punkt).  
Beispiel zur Überprüfung einer Funktion auf punktsymmetrie zu einem bestimmten Punkt
  • Vereinfacht das dann soweit wie möglich: 
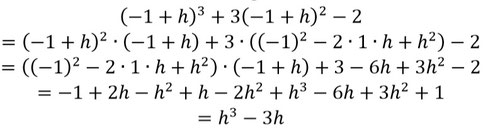
Ausführlicher Rechenweg zur Überprüfung auf Punktsymmetrie
  • Jetzt setzt ihr alles genauso in die Gleichung von Schritt 2 ein: 
Einsetzen in den zweiten Teil der Formel zur Überprüfung auf Punktsymmetrie
  • Vereinfacht das dann wieder soweit wie möglich:
Ausführlicher Rechenweg zum zweiten Teil der Überprüfung auf Punktsymmetrie

Wie ihr jetzt seht, kommt bei beiden Formeln dasselbe raus, also ist die Funktion zum Punkt (-1|2) symmetrisch.

Grafische Darstellung einer punktsymmetrischen Funktion

Aufgaben zur Punktsymmetrie von Funktionen

Ist die Funktion f(x)=x5 punktsymmetrisch? Einblenden
Ist die Funktion f(x)=(x+3)3-1 punktsymmetrisch? Einblenden

Weitere Aufgaben zur Symmetrie

Aufgaben zu diesem Thema findet ihr über den Button unten. Dort könnt ihr euch Arbeitsblätter downloaden. Lösungen zu den Aufgaben findet ihr dort ebenfalls:

Arbeitsblätter zur Symmetrie von Funktionen

Relevante Themen zur Symmetrie

Passende Lernmaterialien

In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.

Mathe Spickzettel in gedrucktem Format

Mathe Spickzettel

Mathe Themenübersichten zum kompakten Lernen.

Mathe Kompakt

Mathe Trainingsbücher zum einfachen Üben.

Mathe Trainingsbücher