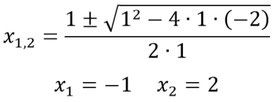Schnittpunkte von Funktionen

Um die Schnittpunkte zu berechnen, folgt einfach diesen Schritten:

  1. Setzt die Funktionsgleichungen gleich
  2. Formt das dann so um (Äquivalenzumformung), ...
    • ... dass das x auf einer Seite alleine steht und berechnet den Rest, das ist dann die x-Koordinate des Schnittpunkts.
    • Außer es ist eine quadratische Funktion darunter, dann müsst ihr so umformen, dass alles auf einer Seite der Gleichung steht und auf der Anderen die Null. Dann könnt ihr x mit der Mitternachtsformel ausrechnen. 
  3. Setzt die x-Koordinate die ihr so erhaltet in eine der beiden Funktionen vom Anfang ein, so erhaltet ihr auch die y-Koordinate.

Schnittpunkte linearer Funktionen

Beispiel: Schnittpunkt von linearen Funktionen berechnen

  • Ihr habt diese zwei Funktionen und wollt ihre Schnittpunkte wissen.
Zwei Funktionen, welche sich schneiden

  • Setzt also zunächst beide Funktionen gleich. 
Lösungsansatz zur Berechnung der Schnittpunkte zweier Funktionen

  • Formt so um, dass das x alleine auf einer Seite steht. So habt ihr die x-Koordinate des Schnittpunktes. 
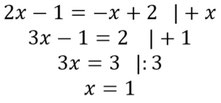
Ausführlicher Rechenweg zur Berechnung der Schnittpunkte von zwei Funktionen

  • Setzt diesen x-Wert in eine der beiden Funktionen vom Anfang ein und berechnet das y. Hier wurde es in g(x) eingesetzt.
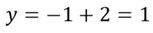
Y-Wert des Schnittpunkts von zwei Funktionen

  • Also hat der Schnittpunkt diese Koordinaten. 
Angabe der Koordinaten des Schnittpunkts von zwei Funktionen

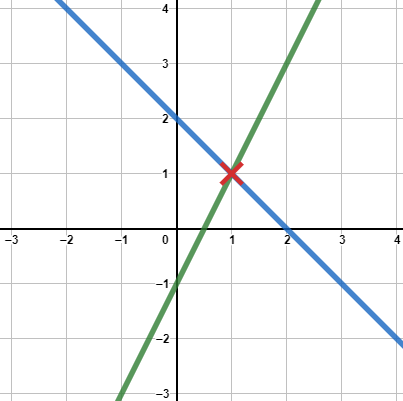
Schnittpunkt von zwei linearen Funktionen grafisch dargestellt mit Markierung des Schnittpunktes

Gezeichnet sehen die Funktionen so aus (f(x) grün und g(x) blau): 


2. Beispiel zur Berechnung von Schnittpunkten

  • Jetzt zeigen wir euch, wie man den Schnittpunkt dieser beiden Funktionen berechnet.

f(x)=2x-2;   g(x)=-2x+2


  • Setzt beide Funktionen gleich und berechnet so das x. Das ist die x-Koordinate des Schnittpunktes.

2x-2=-2x+2  |+2+2x

4x=4  |:4

x=1


  • Setzt das x jetzt in eine der beiden Funktionen vom Beginn ein, so erhaltet ihr die y-Koordinate des Schnittpunktes.

y=2·1-2=0


  • Jetzt kennt ihr die Koordinaten des Schnittpunktes.

S(1|0)


Grafische Darstellung des Schnittpunkts zweier Funktionen

Hier seht ihr die beiden Funktionen eingezeichnet mit ihrem Schnittpunkt.


Aufgaben: Schnittpunkte linearer Funktionen berechnen

Hier könnt ihr mit zwei Aufgaben üben, oder euch einfach weitere Beispiele angucken, klickt auf "Einblenden", um die Lösung zu sehen:

f(x)=2x+1; g(x)=x-2 Einblenden
f(x)=5x+4; g(x)=3x+5 Einblenden

Schnittpunkte einer quadratischen und linearen Funktion berechnen

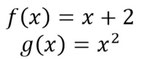
Beispiel für eine lineare und eine quadratische Funktion, welche sich in zwei Punkten schneiden
  • Es sollen die Schnittpunkte dieser beiden Funktionen berechnet werden.

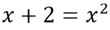
Lösungsansatz zur Berechnung von beiden Schnittpunkten
  • Setzt die Funktionen gleich.

Umformung der Gleichung, sodass die Null auf einer Seite steht
  • Formt die Gleichung so um, dass alles auf einer Seite steht und auf der Anderen die Null. 

Einsetzen der Gleichung in die Mitternachtsformel
  • Berechnet das x mit der Mitternachtsformel. Diese x-Werte sind die x-Koordinaten der Schnittpunkte. 

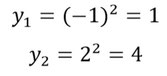
Berechnung der y-Werte der beiden Schnittpunkte
  • Setzt die x-Werte in eine der beiden Funktionen vom Anfang ein, und ihr erhaltet so die y-Werte. Hier wurden sie in g(x) eingesetzt. 

Angabe beider Schnittpunkte in Koordinatenschreibweise
  • Das sind dann die Koordinaten der Schnittpunkte. 

Gezeichnet sehen die Funktionen so aus: 

Grafische Darstellung der Schnittpunkte einer linearen und einer quadratischen Funktion

Aufgaben zur Berechnung von Schnittpunkten

Aufgaben zu diesem Thema findet ihr über den Button unten. Dort könnt ihr euch Arbeitsblätter downloaden. Lösungen zu den Aufgaben findet ihr dort ebenfalls:

Arbeitsblätter zu Schnittpunkten

Relevante Themen