Quadratische Funktionen
Quadratische Funktionen sind Funktionen, bei denen das x quadriert wird. Dabei können sie zwei Formen haben:
Allgemeine Form:
Scheitelpunktform:
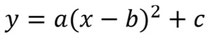
Sie beschreiben Parabeln und heißen quadratisch, da das x quadriert wird.
Beispiele von quadratischen Funktionen
y=x2
y=2x2+x-3
y=2(x-3)2+2
Wie wirken sich die Parameter a,b und c auf die Parabeln aus?
Die Scheitelform eignet sich am besten dafür, um zu erkennen, wo die Parabel liegt, sie ist gegeben durch:
y=a(x-b)2+c
Der Streckungsfaktor a:
- Je größer der Betrag von a ist (also egal ob positiv oder negativ, je weiter a "von der 0 weg ist"), desto steiler/"enger" ist die Parabel
- Je kleiner der Betrag von a ist (also je näher die Zahl der 0 ist), desto breiter wird die Parabel
- Ist a positiv, ist die Parabel nach oben geöffnet
- Ist a negativ, ist die Parabel nach unten geöffnet
Verschiebung in x-Richtung durch b:
- Ist b negativ, wird die Parabel nach links um den Wert von b verschoben (es steht dann ein + zwischen dem x und dem b, denn - mal - gibt +)
- Ist b positiv, wird die Parabel nach rechts um den Wert von b verschoben (es steht ein - zwischen dem x und dem b)
Verschiebung in y-Richtung durch c:
- Ist c positiv, wird die Parabel um c nach oben verschoben
- Ist c negativ, wird die Parabel um c nach unten verschoben
Wie bestimme ich die Nullstellen
Wie man Nullstellen bestimmt und Übungsblätter zu diesem Thema findet ihr hier:
Wie bestimme ich den Scheitelpunkt?
Der Scheitelpunkt ist der höchste/tiefste Punkt einer Parabel. Um den Scheitelpunkt zu bestimmen, müsst ihr die Funktionsgleichung in die Scheitelpunktform umwandeln, falls sie noch nicht in dieser Form gegeben ist. Dann könnt ihr den Scheitelpunkt einfach ablesen, nämlich ist bei y=a(x-b)2+c ...
- ... b die x-Koordinate des Scheitels.
- ... c die y-Koordinate des Scheitels.
Also liegt der Scheitelpunkt dann bei S(bIc). Also geben einem b und c dann gleich den Scheitel an.
Nur was, wenn die Funktion in der allgemeinen Form ist? Dann muss man die quadratische Ergänzung durchführen und erhält so dann die Scheitelform.
Beispiele:
-
y=2(x-3)2+2 -> Hier ist der Scheitel bei (3|2), dies könnt ihr auch oben in der Zeichnung sehen.
- y=3(x+4)2-3-> Hier ist der Scheitel bei (-4|-3). Denn damit in der Klammer x+4 steht, muss b ja negativ sein, denn - mal - gibt +!
Aufgaben zur Bestimmung des Scheitelpunktes
Hier sind Übungsaufgaben, bzw. Beispiele, mit Lösungen. Klickt auf Einblenden für den Lösungsweg:
| Wo liegt der Scheitelpunkt bei der Funktion f(x)=2(x-2)2-2 | Einblenden | |
| Wo liegt der Scheitelpunkt bei der Funktion f(x)=3(x+1)2-4 | Einblenden | |
Scheitelpunktform bestimmen
Die Scheitelpunktform bestimmt ihr, indem ihr die quadratische Ergänzung durchführt. Wie dies geht, findet ihr hier:
Wie bestimme ich die Umkehrfunktion?
Wie man eine Umkehrfunktion bestimmt, findet ihr im Artikel zur Umkehrfunktion. Die Umkehrfunktion der quadratischen Funktion ist die Wurzelfunktion. Wichtig zur Bestimmung der Umkehrfunktion ist die Äqivalenzumformung.
Weitere Eigenschaften quadratischer Funktionen
Monotonie
Die quadratische Funktion ist bis zu x=0 streng monoton fallend und danach streng monoton steigend. Mehr zu dem Thema Monotonie.
Grenzwerte
Die Grenzwerte für + Unendlich und - Unendlich sind in beiden Fällen + Unendlich. Mehr zu dem Thema Grenzwerte.
Extremstellen
Die Extremstelle der quadratischen Funktion ist der Scheitel und daher immer der auch der Scheitelpunkt. Ist a positiv, ist es ein Tiefpunkt, ist a negativ, ist es ein Hochpunkt
Relevante Themen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
