Produktregel bei der Ableitung

Die Produktregel wird bei Funktionen eingesetzt, bei der zwei Funktionen (bzw. die Teile einer Funktion mit einem x) miteinander multipliziert werden. "Erste Funktion abgeleitet mal die Zweite, plus die erste Funktion mal die Ableitung der Zweiten"

Bei der folgenden Funktion müsst ihr die Produktregel anwenden, da x an sich eine Funktion ist und e^x ebenfalls:

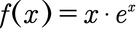
• Jetzt müsst ihr die Produktregel anwenden, also:
• • Als Erstes leitet ihr die erste Funktion ab, also x, das nehmt ihr mal die andere Funktion nicht abgeleitet, also e^x, so erhaltet ihr dann 1·e^x=e^x.
  • Das macht ihr dann genau umgekehrt, also leitet e^x ab und nehmt das mal x. So erhaltet ihr x·e^x.
  • Diese beiden Terme addiert ihr dann zusammen und ihr habt die Ableitung:

Bei dieser Funktion müsst ihr ebenfalls die Produktregel anwenden, da x² und sin(x) zwei einzelne Funkionen sind, die hier multipliziert werden:

• Ihr geht wieder genauso vor:
• • Leitet das Erste ab, mal das andere nicht abgeleitet, also x² ableiten und mal sin(x) nehmen, so erhaltet ihr: 2x·sin(x)
  • Dann macht ihr es genau umgekehrt, also sin(x) ableiten mal x²: x²·cos(x)
  • Das addiert ihr dann, so habt ihr die Ableitung:

Weitere Beispiele:

Hier eine Aufgabe, die ihr auch mal durchrechnen könnt. Klickt auf Einblenden, um die Lösung zu sehen:

Aufgaben zu diesem Thema findet ihr über den Button unten. Dort könnt ihr euch Übungsblätter inklusive Lösungen kostenlos downloaden. 

1. Allgemeine Informationen zur Ableitung
2. Potenz- und Faktorregel
3. Summen- und Differenzregel
4. Kettenregel
5. Quotientenregel

In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.