Potenzfunktion - Eine Übersicht
Eine Potenzfunktion ist eine Funktion der Form:
f(x)=xn
mit n∈ℤ\{0} (das bedeutet man darf alle ganzen Zahlen für n einsetzen, aber nicht die 0). Man darf die Null nicht einsetzen, da sonst immer 1 raus kommen würde, egal was man für x einsetzt, da x0=1 ist. Wie ihr vielleicht schon bemerkt habt, sind die quadratische und lineare Funktion ebenfalls Potenzfunktionen.
Beispiele für Potenzfunktionen
y=x
y=x4
y=x-2
Graphen von Potenzfunktionen
Die Graphen von Potenzfunktionen unterscheiden sich, je nachdem, ob der Exponent gerade, ungerade, positiv oder negativ ist. Hier seht ihr alle Fälle:
Gerader und positiver Exponent:
z.B. f(x)=x2
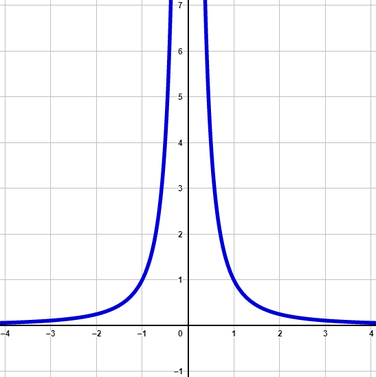
Gerader und negativer Exponent:
z.B. f(x)=x-2
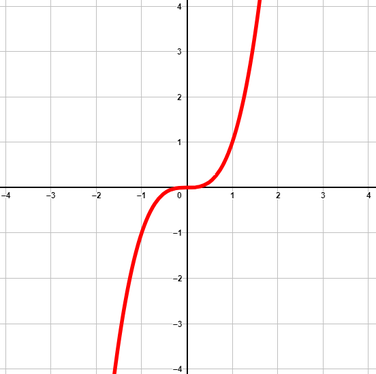
Ungerader und positiver Exponent:
z.B. f(x)=x3
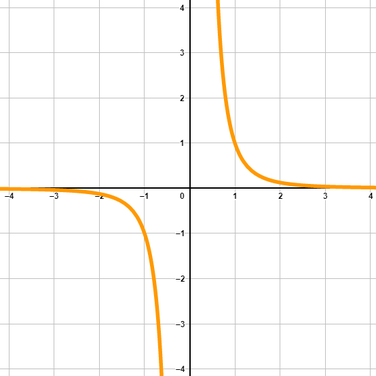
Ungerader und negativer Exponent:
z.B. f(x)=x-3
Eine Potenzfunktion der Form:
f(x)=a·xn
kann verschiedene Graphen beschreiben, hier seht ihr welchen Graphen sie wann abbildet:
1. Gerade (n=1)
- Ist n=1 so ist die Funktion linear und es ergibt sich eine Gerade.
- f(x)=a·x1 =a·x
2. Parabel (n>1)
-
Ist n>1 so ergeben sich Parabeln, z.B.: f(x)=a·x2
- Man nennt diese dann Parabeln n-ter Ordnung. Bei unserem Beispiel wäre es also eine Parabel 2-ter Ordnung.
3. Hyperbel (n<0)
- Ist n<0, also Minuszahlen, ergeben sich Hyperbeln.
- Diese nennt man dann auch Hyperbeln n-ter Ordnung. Das hier wäre eine Hyperbel 3. Ordnung: f(x)=a·x-3
4. Faktor a
- Das a bewirkt nur, dass die Funktion steiler wird, wenn das a groß ist und flacher, wenn a klein ist.
Hier geht´s zur Wurzelfunktion, die eine spezielle Form der Potenzfunktion ist.
Definitions- und Wertemenge
Die Definitions- und Wertemenge hängt davon ab, ob der Exponent gerade, oder ungerade ist, und ob positiv oder negativ. Hier seht ihr die jeweilige Definitions- und Wertemengen:
Gerader und positiver Exponent:
- D=ℝ
- W=ℝ0+
Gerader und negativer Exponent:
- D=ℝ/{0}
- W=ℝ+
Ungerader und positiver Exponent:
- D=ℝ
- W=ℝ
Ungerader und negativer Exponent:
- D=ℝ/{0}
- W=ℝ/{0}
Symmetrie
Die Symmetrie hängt ebenfalls davon ab, ob der Exponent positiv oder negativ ist. Eine ausführliche Erklärung zur Symmetrie findet ihr im Artikel zur Symmetrie.
Gerader Exponent:
- achsensymmetrisch (zur y-Achse)
Ungerader Exponent:
- punktsymmetrisch (zum Koordinatenursprung)
Grenzwerte
Die Grenzwerte einer Potenzfunktion sind ebenfalls von ihrem Exponent abhängig:
Gerader und positiver Exponent:
-
limx→∞f(x)=∞
-
limx→-∞f(x)=∞
-
limx→+0f(x)=0
-
limx→-0f(x)=0
Gerader und negativer Exponent:
-
limx→∞f(x)=0
-
limx→-∞f(x)=0
-
limx→+0f(x)=∞
-
limx→-0f(x)=∞
Ungerader und positiver Exponent:
-
limx→∞f(x)=∞
-
limx→-∞f(x)=-∞
-
limx→+0f(x)=0
-
limx→-0f(x)=0
Ungerader und negativer Exponent:
-
limx→∞f(x)=0
-
limx→-∞f(x)=0
-
limx→+0f(x)=∞
-
limx→-0f(x)=-∞
Monotonie
Die Monotonie hängt, wie so vieles, auch vom Exponenten ab, hier alle Fälle:
Gerader und positiver Exponent:
- strengmonoton fallend bis 0
- strengmonoton steigend ab 0
Gerader und negativer Exponent:
- strengmonoton steigend (komplett)
Ungerader und positiver Exponent:
- strengmonoton steigend bis 0
- strengmonoton fallend ab 0
Ungerader und negativer Exponent:
- strengmonoton fallend (komplett)
Passende Themen zu Potenzfunktionen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
