Partielle Integration
Die partielle Integration (oder auch Produktintegration) ist der Produktregel beim Ableiten ähnlich, es ist sozusagen die Umkehrung dieser. Sie ist ein Hilfsmittel, um Funktionen integrieren zu können, wenn die Funktion selbst aus zwei Funktionen (z.B. sin(x) und x) besteht, welche multipliziert werden:
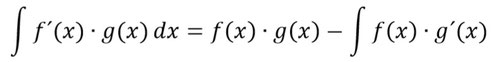
- f´(x) wird aufgeleitet und zu f(x)
- g(x) wird abgeleitet und zu g´(x)
Berechnung der partiellen Integration
Das Vorgehen bei der partiellen Integration ist Folgendes:
- Die Funktion muss aus zwei Faktoren bestehen, ihr betrachtet beide dann als "einzelne Funktionen" (f´(x) und g(x)).
- Die partielle Integration ist nur sinnvoll, wenn eines der beiden Produkte leicht aufzuleiten ist und das andere beim Ableiten vereinfacht wird (z.B. x, denn wenn man x ableitet, wird es 1).
- Dabei ist das leicht aufzuleitende f´(x) …
- … und das, was sich beim Ableiten vereinfacht, g(x).
- Leitet das, was leicht zu integrieren ist, auf und das Andere ab.
- Setzt das, alles wie oben in der Formel ein und berechnet das letzte Integral, dann seid ihr fertig.
Beispiel zur Berechnung der partiellen Integration
Dieses Integral kann zum Beispiel partiell integriert werden.

Stellt zuerst fest, welcher der beiden Faktoren aufgeleitet (f´(x)), bzw. abgeleitet werden soll (g(x)). Der Faktor, welcher durch das Ableiten vereinfacht wird, sollte abgeleitet werden (hier g(x)=x) und der Andere aufgeleitet (hier f´(x)=sin(x)).

Führt dann die Auf- bzw. Ableitung dieser beiden Funktionen durch. Mehr zum Thema findet ihr unter Ableitungsregeln.
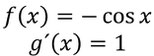
Setzt dann beide so erhaltenen Funktionen in die Formel der partiellen Integration ein.
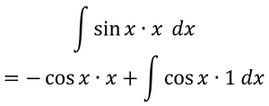
Berechnet nun das übrig gebliebene Integral. Das ist nun die Stammfunktion.
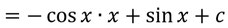
2. Beispiel: partielle Integration berechnen
Nun soll dieses Integral partiell integriert werden.
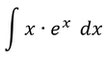
Der erste Schritt ist wieder festzustellen, welcher der beiden Faktoren aufgeleitet (f´(x)), bzw. abgeleitet werden soll (g(x)). Denjenigen Faktor, der durch die Ableitung vereinfacht wird, solltet ihr dann ableiten (hier x) und den Anderen aufleiten (hier ex).

Leitet f(x) dann auf und g(x) ab.

Setzt die beiden Funktionen dann in die Formel der partiellen Integration ein.
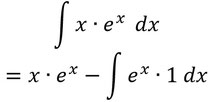
Berechnet nun das übrig gebliebene Integral.

Das, was dann rauskommt, ist euer Ergebnis des Integrals von oben.
Tipps
Hier zwei Tipps für die partielle Integration:
- Wenn ein Faktor x ist, ist dieser immer g(x). Das ist der Teil, der dann abgeleitet wird. Das x fällt nämlich beim Ableiten weg (wird 1, siehe Beispiel 1).
- Wenn Cos, Sin oder ex vorkommt, sind diese (meist) f´(x), da diese leicht zu integrieren sind.
Mehrfache Ausführung der partiellen Integration
Sollte nach dem partiellen Integrieren das hinten dran entstandene Integral nicht einfach zu berechnen sein, müsst ihr manchmal die partielle Integration für dieses Integral noch einmal durchführen.
Beispiel: partiellen Integration mehrfach durchführen
Jetzt soll dieses Integral partiell integriert werden.
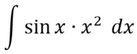
- Stellt zuerst fest, welcher der beiden Faktoren aufgeleitet (f´(x)), bzw. abgeleitet werden soll (g(x)). Den, welcher durch Ableiten vereinfacht wird, solltet ihr dann ableiten (hier x2) und den Anderen aufleiten (hier sin(x)):

- Führt dann die Auf- bzw. Ableitung dieser beiden Funktionen durch:

- Setzt dann beide so erhaltenen Funktionen in die Formel der partiellen Integration ein:

- Jetzt müsst ihr das hintere Integral noch berechnen, aber wie ihr seht, geht es hier nicht so einfach, deshalb müsst ihr noch mal die partielle Integration für dieses Integral anwenden:
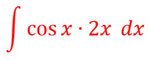
- Also wieder feststellen, welcher Teil aufgeleitet und welcher abgeleitet wird:
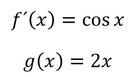
- Dann auf- und ableiten:

- In die Formel für partielle Integration einsetzen:

- Das setzt ihr jetzt für das Integral nach der ersten partiellen Integration ein, dann seid ihr fertig:

Jetzt habt ihr das Integral fertig berechnet.
Wann ist die partielle Integration hilfreich?
Dann, wenn folgende Bedingungen erfüllt sind:
- Wenn die zu integrierende Funktion aus zwei Faktoren besteht und beide für sich eine Funktion bilden (also beide Faktoren ein x enthalten).
- Wenn der eine Faktor leicht zu integrieren ist und der Andere beim Ableiten vereinfacht wird, z.B. x wird zu 1.
- Wenn durch mehrfaches partielles Integrieren der eine Teil beim Integrieren nie erschwert wird, was zum Beispiel beim Sinus, Cosinus und der e-Funktion der Fall ist und der andere Teil nach mehrfachem Ableiten wegfällt (z.B. x2, x3, x4…)
