Wendepunkte und Krümmungsverhalten
Wendepunkte berechnen
An den Wendestellen/punkten ändert sich die Krümmung. Um sie zu berechnen, geht ihr so vor:
- Ableitung bestimmen und dann diese noch mal ableiten (also die 2. Ableitung bestimmen)
- die Nullstellen der 2. Ableitung bestimmen, das sind die x-Koordinaten der Wendepunkte.
- Setzt nun nur noch die x-Koordinate für Wendepunkte in die ursprüngliche Funktion ein, um die y-Koordinate zu bestimmen. Wollt ihr nur diese wissen, seid ihr jetzt fertig.
- Um zu bestimmen, ob es ein Rechts-Links-Wendepunkt ist oder ein Links-Rechts Wendepunkt, bestimmt ihr die 3. Ableitung, also noch mal die 2. Ableitung ableiten
- Setzt für x die x-Koordinate des Wendepunktes in die 3. Ableitung ein (wenn kein x da ist, guckt euch nur das Ergebnis an), ist das Ergebnis:
- f´´´(x)>0 rechts-linksgekrümmt
- f´´´(x)<0 links-rechtsgekrümmt
- f´´´(x)=0 es ist eine genauere Betrachtung der Krümmung nötig, z. B. durch eine Zeichnung.

Hier seht ihr den Wendepunkt W und wie die Funktion vor dem Wendepunkt rechtsgekrümmt ist und danach linksgekrümmt. Also ist die Funktion rechts-linksgekrümmt.
Beispiel zur Berechnung von Wendepunkten
Nun "wollt" ihr die Wendestellen/punkte der Funktion bestimmen:
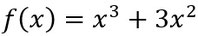
- Erst mal bestimmt ihr die 2. Ableitung

- Danach bestimmt ihr die Nullstellen der 2. Ableitung, das sind eure Wendepunkte!:
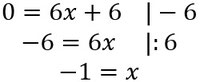
- Also ihr habt einen Wendepunkt mit dieser x-Koordinate. Um die y-Koordinate zu erhalten, setzt ihr den x-Wert in die Funktion ein und rechnet dies aus:
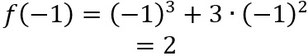
- Die Koordinaten des Wendepunktes sind also:

- Um zu bestimmen, ob es ein links-rechts oder rechts-links Wendepunkt ist, bestimmt ihr die 3. Ableitung.

- Da man hier kein x einsetzen kann, guckt ihr euch die Ableitung an sich an. Sie ist positiv, also ist es ein rechts-links Wendepunkt.


Hier seht ihr die Funktion aus dem Beispiel. Am Wendepunkt ändert sich die Krümmung, welche erst rechts- und dann links gekrümmt ist.
Beispiel 2 / Übungsaufgabe: Wendepunkte berechnen
Klickt auf Einblenden, um die Lösung zu sehen. Ihr könnt diese Aufgabe auch als Übung machen und dann nachgucken, ob ihr sie richtig habt:
| Wendepunkt von f(x)=x3+3x2 | Einblenden | |
|
Lösung:
|
||
Aufgaben zum Üben
Ihr könnt euch kostenlos Aufgaben zum Üben der Wendepunkte downloaden und ausdrucken:
Krümmungsverhalten berechnen
Das Krümmungsverhalten einer Funktion sagt aus, wie diese in ihrem Verlauf gekrümmt ist. Um das Krümmungsverhalten zu bestimmen, müsst ihr ableiten können. Unter Ableitung könnt ihr das nochmal wiederholen.
Es gibt folgende Krümmungen:
- rechts gekrümmt / konkav / im Uhrzeigersinn gekrümmt
-
- dies ist der Fall, wenn die 2. Ableitung f´´(x)<0
- links gekrümmt / konvex / gegen Uhrzeigersinn gekrümmt
-
- dies ist der Fall, wenn die 2. Ableitung f´´(x)>0

Vorgehen beim Bestimmen vom Krümmungsverhalten:
- Ableitung bestimmen und dann diese noch mal ableiten (also die 2. Ableitung bestimmen)
- Die Nullstellen der 2. Ableitung bestimmen (gibt es keine, dann heißt das die Funktion ist immer gleich gekrümmt)
- An den Nullstellen ändert sich das Krümmungsverhalten (das sind die Wendepunkte, dazu oben mehr).
- Werte vor und nach den Nullstellen in die 2. Ableitung einsetzen und gucken, ob sie positiv oder negativ sind.
- Ist der Wert negativ, ist die Funktion rechts gekrümmt
- Ist der Wert positiv, ist die Funktion links gekrümmt
- Die Krümmung der Funktion bleibt dann den ganzen Bereich bis bzw. ab den Nullstellen der 2. Ableitung gleich! Gibt es keine Nullstellen bei der 2. Ableitung, dann ist die Funktion immer gleich gekrümmt.
Beispiel: Krümmungsverhalten bestimmen
Mal angenommen, ihr "wollt" das Krümmungsverhalten folgender Funktion wissen, da es euch so unglaublich interessiert:

- Leitet die Funktion erst mal 2 mal ab (weiter unten ist ein Ableitungsrechner ;):

- Danach bestimmt ihr die Nullstellen der 2. Ableitung. Das sind eure Wendepunkte, also ab da ändert sich die Krümmung, davor ist sie immer gleich und danach auch, bis zum nächsten Wendepunkt:

- Also das ist euer Wendepunkt. Jetzt müsst ihr nur noch gucken, wie die Funktion vor und nach dem Wendepunkt gekrümmt ist, setzt einfach mal eine Zahl vor dem Wendepunkt und einen danach in die 2. Ableitung ein, z.b. -1 und 1. Dann seht ihr, vor dem Wendepunkt ist die 2. Ableitung negativ, also ist sie da rechts gekrümmt, und danach positiv, also links gekrümmt.


Hier seht ihr die Funktion aus dem Beispiel. Sie ist erst rechts gekrümmt und danach links gekrümmt.
Terrassen/Sattelpunkt
Um den Terrassenpunkt zu bestimmen, muss nur eine Bedingung noch zusätzlich zu denen eines Wendepunktes gelten, nämlich das die erste Ableitung an der Stelle des Wendepunktes Null ist. Also hier die Übersicht, was alles gelten muss, damit es ein Terrassen/Sattelpunkt ist:
- f´(x)=0
- f´´(x)=0
- f´´´(x)≠0
