Koordinatensysteme in der Mathematik
Koordinatensysteme sind dafür da, Positionen in einem Raum zu beschreiben, wenn man so will sind Straßen und Hausnummern auch Koordinatensysteme. In der Mathematik verwendet man diese dann, um mathematische Strukturen zu veranschaulichen, denn da geht es auch um Punkte in einem Raum.
Kartesisches Koordinatensystem
Das kartesische Koordinatensystem kennt ihr bestimmt schon. Es besteht aus zwei Achsen, der x- und y-Achse, welche senkrecht aufeinander stehen (also im Winkel von 90°). Es werden dann die Koordinaten so aufgetragen, dass einer Zahl auf der x-Achse eine Zahl auf der y-Achse zugeordnet wird. Der Schnittpunkt der x- und y-Achse wird Koordinatenursprung genannt.
Einfaches Koordinatensystem
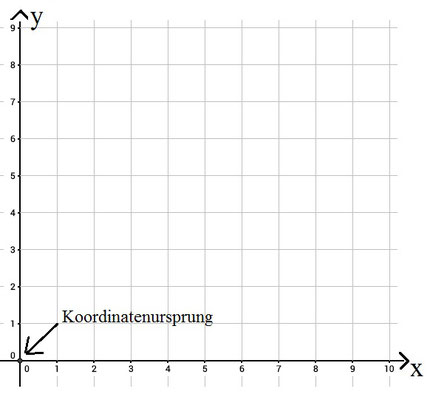
Ein einfaches Koordinatensystem besteht aus der x- und y-Achse und dem Koordinatenursprung, welcher immer beim Schnittpunkt von x- und y-Achse ist und die Koordinaten (0|0) hat.
Koordinatensystem mit Minuszahlen
Ein Koordinatensystem mit Minuszahlen hat zusätzlich noch den negativen Teil der Koordinatenachsen und daher wird es in 4 Quadranten eingeteilt, welche gegen den Uhrzeigersinn eingetragen werden.
Punkte im Koordinatensystem eintragen
Punkte werden meist in der Form angegeben, dass der Name des Punktes vor der Klammer mit den Koordinaten steht, also z.B. so: P(x|y) oder auch P(x,y). Dabei gibt der Wert links die x-Koordinate an und der Wert rechts die y-Koordinate. Wie ihr das dann richtig in ein Koordinatensystem eintragt, seht ihr darunter in einem Beispiel:
Möchtet ihr einen Punkt einzeichnen, macht ihr das so:
- Geht auf der x-Achse (vom Ursprung aus) so weit nach rechts (links bei Minuszahlen), wie es der x-Wert sagt, also zum Beispiel bei A(3|2) geht ihr 3 nach rechts auf der x-Achse.
- Danach geht ihr von dem Punkt, wo ihr gerade seid, so weit senkrecht nach oben (bei Minuszahlen nach unten), wie es euer y-Wert sagt, also bei A(3|2) geht ihr 2 nach oben. Dort liegt dann euer Punkt.
Verwandte Themen:
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
