Integrale berechnen
Es gibt drei wesentliche Arten von Integralen, deren Berechnung im Folgenden erklärt werden.
Unbestimmtes Integral
Das unbestimmte Integral gibt die Stammfunktion an. Es hat keine obere und untere Grenze.
Wenn ein solches Integral da steht, bedeutet es, man soll die Stammfunktion zu der Funktion finden, die zwischen dem Integralzeichen (dieses komische S) und dem dx steht. Diese beiden Teile des Integrals "klammern" die Funktion ein, die man aufleiten soll. Das sieht dann folgendermaßen aus:
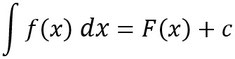
Beispiel:
Hier seht ihr, wie ein unbestimmtes Integral berechnet wird, man bestimmt die Stammfunktion und ist fertig:

Aufgaben und Spickzettel zum unbestimmten Integral
Hier findet ihr Übungsaufgaben und Spickzettel zum unbestimmten Integral:
Bestimmtes Integral
Das bestimmte Integral gibt die Fläche zwischen dem Graphen der Funktion und der x-Achse in einem bestimmten Bereich an (deshalb bestimmtes Integral). Dazu setzt man einen Anfangs- und Endpunkt ein und erhält dann die Fläche unterm Graphen zwischen den beiden Punkten. Wie das aussieht und funktioniert, seht ihr hier:

Dabei ist a der Anfangspunkt (also der kleinere x-Wert) und b der Endpunkt (also der größere x-Wert).
Schritt für Schritt Vorgehen beim berechnen des bestimmten Integrals:
- Stammfunktion berechnen
- Schreibt die Stammfunktion in eckigen Klammern mit dem Anfangs- und Endpunkt am Ende der Klammer. Das +C könnt ihr dabei weglassen, da es sowieso wegfallen würde.
- Um dann das Integral zu berechnen, setzt man den Endpunkt in die Stammfunktion ein und zieht davon die Stammfunktion mit dem eingesetzten Anfangspunkt ab. Das ist dann das Ergebnis des bestimmten Integrals.
Beispiel: bestimmtes Integral berechnen
Um die Fläche unter der Funktion f(x)=x zwischen 1 und 3 zu berechnen, verwendet man das bestimmte Integral wie oben beschrieben. Das Ergebnis ist dann die Fläche unter dem Graphen in diesen Grenzen. Hier ein Beispiel wie man es berechnet:

- Habt ihr so ein Integral, müsst ihr erst mal die Stammfunktion bestimmen, diese schreibt ihr dann in eckigen Klammern mit dem Anfangs- und Endwert hinter der Klammer.

- Jetzt müsst ihr erst den Endwert in die aufgeleitete Funktion für x einsetzen und davon zieht ihr die aufgeleitete Funktion mit eingesetztem Startwert ab. Das ist dann die Fläche unter der Funktion in diesen Grenzen:

Weitere Beispiele zur Berechnung


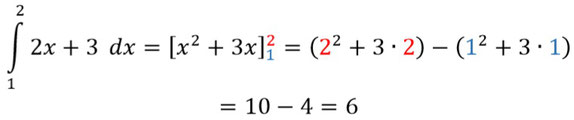
Aufgaben und Spickzettel zum bestimmten Integral
Hier findet ihr Übungsaufgaben und Spickzettel zu den bestimmten Integralen:
Unbeschränkte Integrale (bis Unendlich)
Sollt ihr ein Integral bis unendlich bestimmen, ist das Vorgehen erst mal genauso wie beim Ausrechnen von Integralen, jedoch gibt es am Ende einen entscheidenden Unterschied:
- Stammfunktion bestimmen
- Grenzen ins Integral einsetzten und ausrechnen
- Ihr habt dann irgendwo das Unendlich stehen, ihr müsst einfach dann wie bei den Grenzwerten gucken was passiert, wenn es gegen unendlich geht
- Ist das Unendlich im Nenner, wird dieser Term Null. Ist das Unendlich im Zähler geht die Fläche gegen Unendlich (kommt bei Aufgaben aber eher selten vor, ist ja langweilig).
Beispiel: unbeschränkte Integrale berechnen
Hier ein Beispiel für ein unbeschränktes Integral, also erst mal normal berechnen und dann gucken, was mit dem Unendlich passiert:
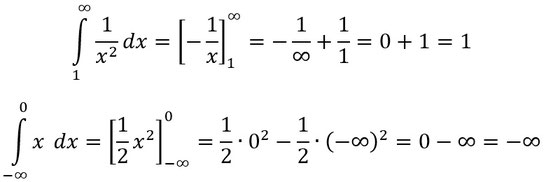
Wie ihr seht, geht der Term mit dem Unendlich gegen 0, also könnt ihr den weglassen und ihr habt das Ergebnis.
