Allgemeines zu Funktionen
Hier beschäftigen wir uns mit der Frage, was Funktionen eigentlich sind und welche Schreibweisen man dabei beachten muss.
Was ist eine Funktion?
Eine Funktion ist eine Zuordnung von zwei Werten, also man weist einem Wert einen Anderen zu, da sie in irgendeinem Zusammenhang stehen, dabei gilt:
- Jedem x aus der Definitionsmenge,...
- ... wird eindeutig... (es gibt nur ein y pro x)
- ... ein y aus der Wertemenge zugeordnet.
Ein Beispiel aus unserem Alltag ist der Preis von Gegenständen, da man der Anzahl an gekauften Gegenständen, einen Preis zuordnet. Je mehr man dann kauft, desto mehr kostet es. Dies wäre dann eine sogenannte lineare Funktion.
Alltagsbeispiel
Ihr geht in einen Supermarkt und möchtet Wassermelonenstücke kaufen. Dabei steht der Preis und die Stücke Wassermelonen in einem Verhältnis, denn je mehr ihr kauft, desto mehr kostet es. Also wird der Anzahl von Wassermelonenstücken (x) ein Preis zugeordnet (y). Dabei kostet ein Wassermelonenstück 2 Euro. So ergeben sich diese Gleichungen:
Jetzt kann man eintragen, wie viele Stücke Wassermelonen man kauft, und erhält den Preis, den man dann zahlen muss. Genau das macht eine Funktion. Man setzt einen Wert ein und erhält den dazugehörigen y-Wert. Die Funktion bei diesem Beispiel wäre y=2x. Dabei ist x die Anzahl an Wassermelonenstücken und y der Preis.
Das könnt ihr dann auch in ein Koordinatensystem eintragen, das blaue unten nennt man dann Funktionsgraphen:
Dabei wird immer der x-Wert nach rechts aufgetragen (x-Achse) und der y-Wert nach oben (y-Achse). Die Funktionsgleichung dieses Beispiels wäre:
y=2x
Wozu braucht man das?
Eine Frage, die ihr bestimmt oft in Mathe stellt, aber wie so oft ist dies wirklich wichtig, denn Funktionen braucht man sehr oft und sie kommen häufig vor. Zum Beispiel bei dem Fall, der oben beschrieben wurde, aber auch in anderen Bereichen, zum Beispiel, wenn ein Auto beschleunigt, das ist dann auch eine Funktion, die beschreibt, in welcher Zeit das Auto wie weit gekommen ist, so kann man dann leicht berechnen, wann das Auto an einer bestimmten Stelle ist. Alles was ihr werft, fahrt oder wenn ihr sonst irgendwas bewegt, kann man es als Funktion darstellen. In der Physik sind daher Funktionen von extrem hoher Bedeutung, aber auch in der Wirtschaft, zum Beispiel, um zu berechnen, wie viel man von etwas verkaufen muss, um Gewinn zu machen.
Schreibweisen
- Man gibt Funktionen Namen, diese bestehen aber immer nur aus einem kleingeschriebenen Buchstaben.
-
- z.B. f oder g
- f: y=2x -> das bedeutet die Funktion, die f heißt, sieht so aus: y=2x
- Das x in der Funktion ist die sogenannte Variable, da kann man dann alle Zahlen einsetzen, die in der Definitionsmenge sind.
- f(x) ist die Funktionsgleichung, man schreibt dies häufig auch statt dem y hin, also zum Beispiel f(x)=2x anstatt f: y=2x. Ist statt dem x eine Zahl in der Klammer, bedeutet es, es ist das Ergebnis für y gemeint, welches rauskommt, wenn man statt x diese Zahl einsetzt und ausrechnet.
- f(x)=y
- f(2) bedeutet, dass in die Funktion f für das x die 2 eingesetzt wurde.
Beispiel: Funktion bestimmen
Ihr geht einkaufen und seht Wassermelonen und denkt euch: "wow geil, perfekt für Matheaufgaben" ;). 1kg Wassermelonen kostet 1€. Jetzt kann man dazu eine Funktion aufstellen, die wir mal f nennen und die sieht so aus: f(x)=1·x (1 Euro pro Kilogramm mal das Gewicht, ergibt den Preis). Diese beschreibt jetzt den Preis (f(x)) bei einem bestimmten Gewicht x. Setzt man nun ein Gewicht für x ein, erhält man den Preis für so viel kg Wassermelonen. Die Funktionsgleichung ist:
f(x)=x
Das könnt ihr dann Zeichnen, indem ihr das Gewicht auf der x-Achse einträgt und dann auf der y-Achse den Preis:
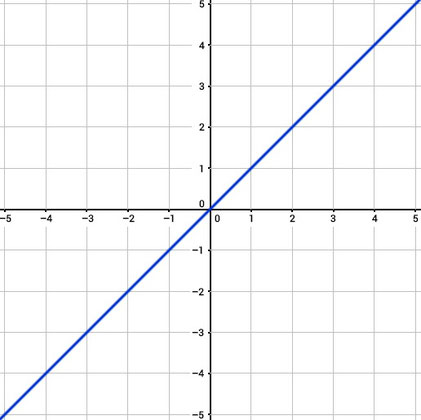
Nun kann man auch direkt ablesen, wie viel zum Beispiel 2kg Wassermelonen kosten, indem man auf der x-Achse bei 2 nach oben geht und guckt, welcher Wert dort bei y steht. Wie ihr seht, gibt es auch einen negativen Bereich, der hat in dieser Aufgabe keinen Sinn, deshalb könnte man diesen auch weglassen. Dieser würde praktisch das Gegenteil von Kaufen sein, also wenn man dem Laden die Wassermelone verkauft und der negative Preis wäre dann das, was man dafür bekommt.
Mehr zu Funktionen
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
