Fläche zwischen zwei Graphen
Wenn man zwei Funktionen hat, die zwischen den Schnittpunkten S1 und S2 eine Fläche einschließen, wobei f(x) bei der gefragten Fläche über g(x) liegt, berechnet man die eingeschlossene Fläche folgendermaßen:

Schritt für Schritt Vorgehen bei der Berechnung
- Macht euch eine Skizze und überlegt euch, welche Funktion über der Anderen liegt (eine ist über der Fläche die berechnet werden soll, die Andere liegt darunter).
- Dann bestimmt ihr die Schnittpunkte der Funktionen. (Dazwischen ist ja die eingeschlossene Fläche)
- Zieht die obere Funktion, von der, die unter ihr liegt, ab. (Eine ist über der Fläche, die berechnet werden soll, die andere liegt darunter)
- Berechnet dann das Integral von dieser "neuen" Funktion und ihr erhaltet die Fläche. Dazu setzt ihr den ersten Schnittpunkt als untere Grenze im Integral ein und den Zweiten als obere Grenze. Dann seid ihr fertig, außer ihr habt mehr als 2 Schnittpunkte der Funktionen, dann geht es hier weiter:
- Haben die Funktionen mehr als zwei Schnittpunkte müsst ihr die Flächen getrennt berechnen, also erst die erste Fläche vom ersten Schnittpunkt bis zum 2. und dann vom 2. Schnittpunkt bis zum 3…. Dann addiert ihr die beiden Flächen. (Passt auf!: einmal ist die eine Funktion oben, dann die Andere, das dürft ihr nicht vergessen)
Beispiel: Fläche zwischen zwei Funktionen berechnen
Ihr möchtet die Fläche, die zwischen diesen Funktionen eingeschlossen wird, berechnen, dabei liegt f über g:
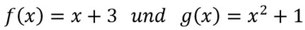
- Bestimmt zunächst die Schnittpunkte, wie das genau geht, findet ihr im Artikel zu Schnittpunkten nochmal.
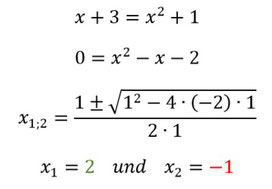
- Habt ihr die Schnittpunkte, zieht ihr die obere Funktion, von der die darunter liegt, ab und integriert diese vom ersten Schnittpunkt bis zum Zweiten. Hier liegt f ja über g und die Schnittpunkte wurden davor berechnet, sie sind -1 und 2:

- Berechnet dies dann und ihr habt eure Lösung, die Fläche zwischen den Graphen:
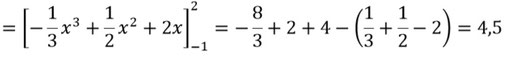
Also ist die eingeschlossene Fläche dieser Funktionen 4,5 Flächeneinheiten groß.
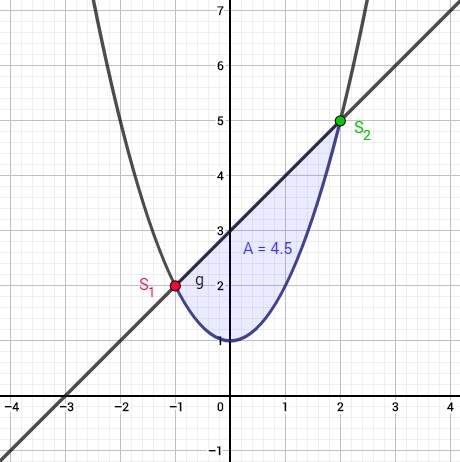
So sehen die Funktionen und die dazwischen eingeschlossene Fläche aus.
2. Beispiel zur Berechnung der eingeschlossenen Fläche
Hier noch ein Beispiel. Ihr möchtet die Fläche zwischen diesen beiden Funktionen berechnen:

- Zunächst berechnet ihr die Schnittpunkte der Funktionen, denn schließlich ist die Fläche genau zwischen den Schnittpunkten. Das sind die Grenzen für die Integration:
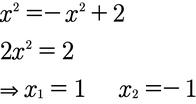
- Nun setzt ihr die Grenzen in das Integral ein und zieht beide Funktionen im Integral voneinander ab, dabei wird f von g abgezogen, da g über der Fläche liegt und f darunter (siehe Bild unten):
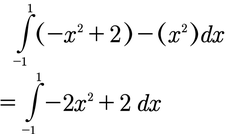
- Dieses Integral rechnet ihr nun aus und ihr habt die Fläche:

- Die Fläche beträgt also 2,66666... FE (Flächeneinheiten).
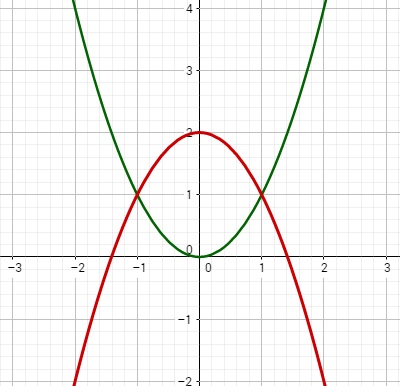
Hier seht ihr die beiden Funktionen, dabei ist f grün und g rot.
