Fläche unter einem Graphen bestimmen
Sollt ihr die Fläche unter einem Graphen mit gegebenen Grenzen berechnen, müsst ihr dies mit dem bestimmten Integral machen. Ist der Graph der Funktion (NICHT Stammfunktion) zwischen den gegebenen Grenzen nur über oder unter der x-Achse?
- Wenn ja, könnt ihr die Grenzen als Anfangs- und Endpunkt in das bestimmte Integral einsetzen und die Fläche berechnen (Bsp. 1).
- Wenn nein (also ist der Graph mal über und mal unter der x-Achse), müsst ihr Folgendes machen (Bsp. 2)
-
- Bestimmt die Nullstelle/n
- Integriert vom Anfangspunkt bis zur Nullstelle
- Dann integriert ihr von der Nullstelle bis zum Endpunkt (außer es gibt mehr Nullstellen, dann integriert ihr bis zur nächsten Nullstelle).
- Addiert eure Ergebnisse (aber nur die Beträge, also ohne Minus!). Das ist dann euer Ergebnis.
Erklärung zur Berechnung der Fläche
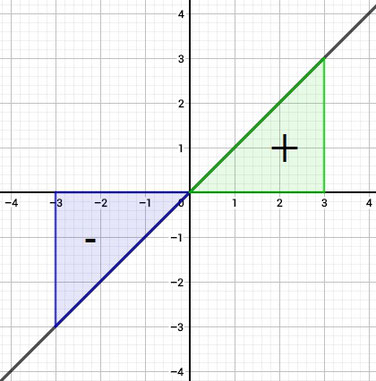
Sollt ihr die Fläche berechnen, müsst ihr jeweils bis zur Nullstelle einzeln integrieren, wenn zwischen End- und Anfangspunkt die Fläche mal über und mal unter der x-Achse liegt. Das liegt daran, da sonst die Fläche von unter der x-Achse von der, die über der x-Achse liegt, abgezogen wird, da die Fläche unter der x-Achse beim Integral immer negativ ist und die über der x-Achse positiv. In diesem Beispiel (Bild) würde sonst 0 für die Fläche rauskommen, da die Fläche unter der x-Achse genauso groß ist, wie die darüber. Also erst die Fläche unter der x-Achse ausrechnen, danach die, die darüberliegt und dann beide Beträge addieren, so erhält man das richtige Ergebnis.
Beispiel: Fläche unter Funktion ohne Vorzeichenwechsel berechnen
Ihr möchtet die Fläche zwischen dieser Funktion und der x-Achse von -2 bis 2 wissen.
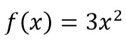
- Diese Funktion ist nie negativ, also auch nur oberhalb der x-Achse, also könnt ihr direkt das Integral aufstellen. Setzt die Grenzen als Anfangs und Endpunkt ein.
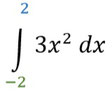
- Bestimmt die Stammfunktion (wie das geht findet ihr unter Stammfunktion):
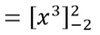
- Jetzt könnt ihr das Integral ausrechnen. Das Ergebnis ist dann die Fläche unter dem Graphen und der x-Achse zwischen 2 und -2.

Hier seht ihr den Graphen und die Fläche dieser Funktion:
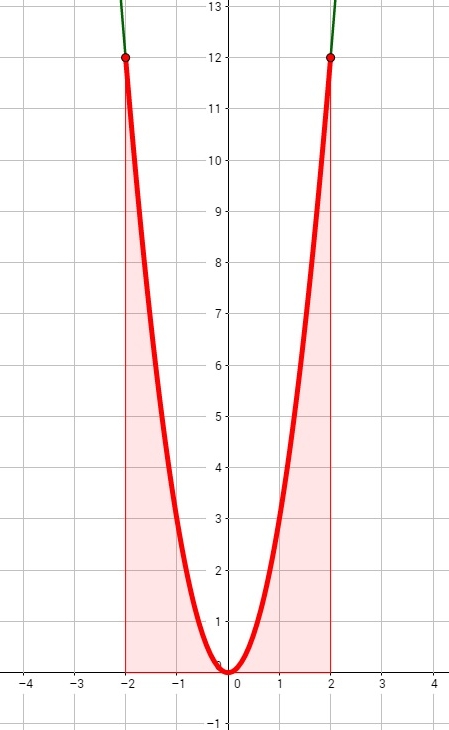
In Rot seht ihr die Fläche, die gerade berechnet wurde. Sie beträgt 16 FE (Flächeneinheiten).
Beispiel: Fläche unter Funktion mit Vorzeichenwechsel berechnen
Ihr möchtet die Fläche dieser Funktion von -2 bis 2 berechnen.
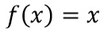
- Ihr bemerkt, dass die Funktion zwischen -2 und 2 nicht nur positiv oder nur negativ ist. Also bestimmt ihr die Nullstelle der Funktion, die zwischen 2 und -2 liegt. Hier ist sie bei x=0.

- Integriert vom Anfangspunkt (-2) bis zur Nullstelle (0).

- Jetzt noch von der Nullstelle bis zum Endpunkt integrieren.

- Jetzt addiert ihr die Beträge der Ergebnisse. Die Fläche unter dem Graphen von -2 bis 2 ist 4FE (Flächeneinheiten) groß.
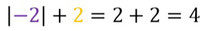
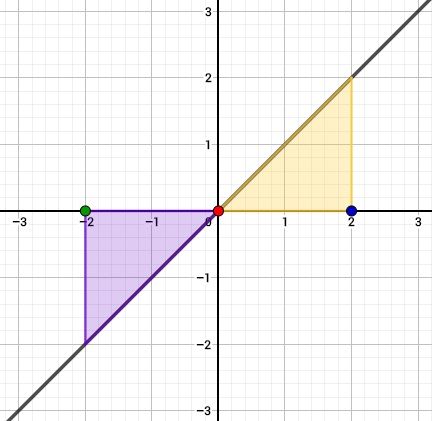
So sieht die Funktion und die Fläche unter dem Graphen vom Beispiel aus. Anfangspunkt ist grün, Nullstelle rot und Endpunkt blau. Die Fläche unter der xAchse ist Lila (wie das Ergebnis beim Rechnen) und über der x-Achse orange (ebenfalls wie das Ergebnis).
Aufgaben zum Üben
Wenn ihr dieses Thema weiter vertiefen und üben möchtet, dann haben wir kostenlose Arbeitsblätter mit Aufgaben für euch. Ihr findet sie unter diesem Button:
