Exponentialfunktion mit Formel und Eigenschaften
Die Exponentialfunktion ist ähnlich der Potenzfunktion, nur dass das x im Exponenten steht, also sieht die Funktion wie folgt aus (mit Vorfaktor b gibt es weiter unten die Erklärung):
f(x)=ax
Wobei a jede positive Zahl außer 0 und 1 sein kann, da sonst die Funktion konstant wäre (also bei a=0 für jedes x immer 0 und für a=1 immer 1).
- ist a zwischen 0 und 1 ist es eine so genannte exponentielle Abnahme, d.h. der Graph fällt ganz schnell und geht gegen 0, nähert sich also der x-Achse immer weiter an, berührt diese aber nie!
- ist a größer als 1, ist es ein so genanntes exponentielles Wachstum, also der Graph steigt schnell an.
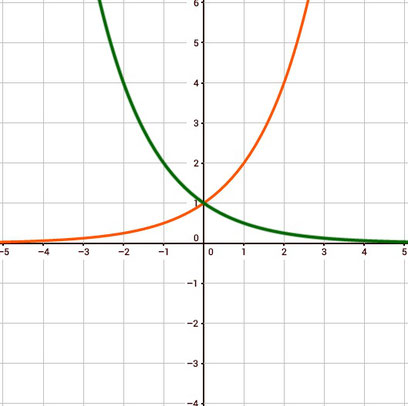
Beispiele einer Exponentialfunktion
y=2x
y=0,5x
Eigenschaften von Exponentialfunktionen
Ist eine Exponentialfunktion in der allgemeinen Form gegeben und nicht verschoben, also in der Form y=ax, ohne Vorfaktor b (unten gibt es dasselbe mit), dann hat sie folgende Eigenschaften:
- sie hat keine Nullstellen
- die x-Achse ist eine waagerechte Asymptote
- sie hat einen Schnittpunkt mit der y-Achse bei (0|1)
Definitions- und Wertemenge
Mehr zu dem Thema findet ihr im Artikel zur Definitions- und Wertemenge. (in der Form y=ax)
- Definitionsmege ist D=ℝ
- Wertemenge ist W=ℝ+
Monotonie
Mehr zu dem Thema findet ihr im Artikel zur Monotonie. (in der Form y=ax)
- Ist a<1, dann ist die Funktion streng monoton fallend.
- Ist a>1, dann ist die Funktion streng monoton steigend.
Grenzwerte
Mehr zu dem Thema findet ihr im Artikel zu den Grenzwerten. (in der Form y=ax)
- Ist a<1, dann ist der Grenzwert für x gegen - Unendlich + Unendlich und für x gegen + Unendlich 0.
- Ist a>1, dann ist der Grenzwert für x gegen - Unendlich 0 und für x gegen + Unendlich +Unendlich.
Umkehrfunktion
Die Umkehrfunktion der Exponentialfunktion ist die sogenannte Logarithmusfunktion. Weitere Informationen findet ihr im Artikel zu Logarithmusfunktionen.
Exponentialfunktion mit Vorfaktor b
Hat die Exponentialfunktion einen Vorfaktor b, muss man bei den Eigenschaften genauer hinschauen, da sich manche Werte verändern können. Die Exponentialfunktion sieht dann so aus:
f(x)=b·ax
Dabei kann das b jede beliebige Zahl sein. Dabei gilt:
- je größer b, desto steiler steigt/fällt die Funktion
- je kleiner b, desto flacher ist der Graph
Ist b positiv:
- ist a zwischen 0 und 1 ist es eine exponentielle Abnahme
- ist a>1 ist es ein exponentielles Wachstum.
Ist b negativ:
- ist a zwischen 0 und 1 ist es eine exponentielle Zunahme
- ist a>1 ist es ein exponentielle Abnahme.
b positiv und a>1
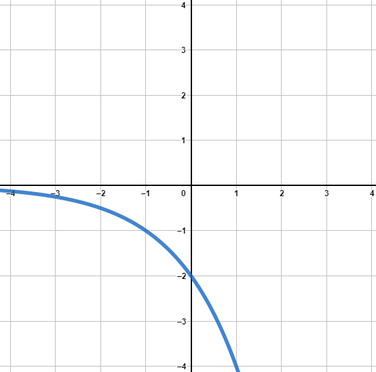
b negativ und a>1
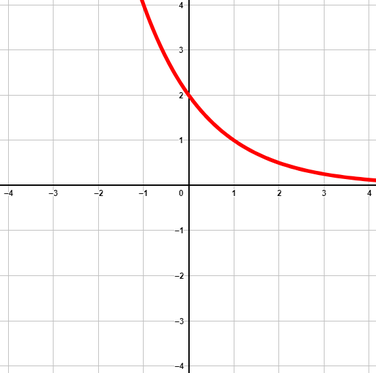
b positiv und a<1
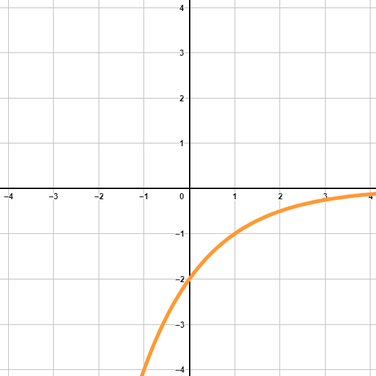
b negativ und a<1
Eigenschaften mit Vorfaktor b
Definitions- und Wertemenge mit Vorfaktor
Mehr zu dem Thema findet ihr im Artikel zur Definitions- und Wertemenge.
Mit positivem Vorfaktor b
- Definitionsmege ist D=ℝ
- Wertemenge ist W=ℝ+
Mit negativem Vorfaktor b
- Definitionsmege ist D=ℝ
- Wertemenge ist W=ℝ-
Grenzwerte mit Vorfaktor
Mehr zu dem Thema findet ihr im Artikel zu den Grenzwerten.
Mit positivem Vorfaktor b
- Ist a<1, dann ist der Grenzwert für x gegen - Unendlich - Unendlich und für x gegen + Unendlich 0.
- Ist a>1, dann ist der Grenzwert für x gegen - Unendlich 0 und für x gegen + Unendlich -Unendlich.
Mit negativem Vorfaktor b
- Ist a<1, dann ist der Grenzwert für x gegen - Unendlich - Unendlich und für x gegen + Unendlich 0.
- Ist a>1, dann ist der Grenzwert für x gegen - Unendlich 0 und für x gegen + Unendlich - Unendlich.
Monotonie mit Vorfaktor
Mehr zu dem Thema findet ihr im Artikel zur Monotonie.
Für positive b
- Ist a<1, dann ist die Funktion streng monoton fallend.
- Ist a>1, dann ist die Funktion streng monoton steigend.
Für negative b
- Ist a<1, dann ist die Funktion streng monoton steigend.
- Ist a>1, dann ist die Funktion streng monoton fallend.
Relevante Themen zur Exponentialfunktion
Passende Lernmaterialien
In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.
