Definitions- und Wertemenge

Definitionsmenge

Die Definitionsmenge gibt an, welche Werte (Zahlen) man in die Funktion (für das x) einsetzen darf. Alle diese Zahlen, die man für x einsetzen darf, sind dann die Definitionsmenge.

Möchtet ihr nun die Definitionsmenge „herausfinden“, guckt ihr, welche Zahlen man nicht einsetzen darf. Es darf nämlich keine…:

… Null im Nenner stehen.
… negative Zahl unter der Wurzel stehen.
… negative Zahl (oder die Null) logarithmiert werden.

Die Zahlen, bei denen eines der beiden Fälle zutrifft, sind nicht in der Definitionsmenge. Sonst darf man alle Zahlen in die Definitionsmenge einsetzen.

Beispiele zur Definitionsmenge

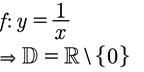
Beispiel der Definitionsmenge einer Bruchfunktion.

Die Definitionsmenge dieser Funktion bestimmt ihr, indem ihr überlegt, was ihr alles für x einsetzen dürft. Hier dürft ihr ja alles einsetzen, außer die Null, denn man darf ja nicht durch 0 Teilen!

Beispiel der Definitionsmenge mit dem x im Nenner.

Geht genauso vor wie oben, welche Zahlen dürft ihr für x einsetzen? Alle außer -1, da ihr schließlich nicht durch 0 teilen dürft.

Hie dürft ihr ja alle positiven Zahlen und die Null einsetzen, negative ja nicht, da man davon nicht die Wurzel ziehen kann.

	Was ist die Definitionsmenge von f(x)=2x-1?	Einblenden
Lösung: D=ℝ → Man kann ja für x jede Zahl einsetzen

	Was ist die Definitionsmenge von f(x)=√x?	Einblenden
Lösung: D=ℝ₀⁺ → Man kann ja für x jede positive Zahl einsetzen und die 0. Es darf nämlich keine negative Zahl unter Wurzel stehen.

Wertemenge

Die Wertemenge gibt an, was alles für y, bzw. f(x), rauskommen kann, wenn man jede Zahl aus der Definitionsmenge in die Funktion (für x) eingesetzt hat. Auch hier guckt man am besten, was nicht rauskommen kann, achtet dabei vor allem auf Folgendes:

Wird x mit einer geraden Zahl potenziert, können nur positive Zahlen (und die 0) rauskommen (z.B. hoch 2).
Wird die Wurzel von x gezogen, kann ebenfalls nur etwas Positives (oder die 0) rauskommen (wenn der Wurzelexponent gerade ist, z.B. die 2. Wurzel).
Ist x im Nenner eines Bruches, bei dem der Zähler nicht 0 werden kann, dann kann die 0 nicht in der Wertemenge sein, da die Funktion dann nie 0 wird.
Für Cosinus und Sinus können nur Werte zwischen -1 und 1 rauskommen.
Ist x im Exponenten kann (bei positiver Basis) nur was Positives rauskommen. Also keine negativen Werte oder die 0.

Beispiele zur Wertemenge

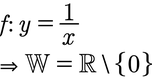
Beispiel der Wertemenge einer Bruchfunktion

Überlegt euch, welche Zahlen rauskommen können, wenn ihr die Definitionsmenge einsetzt. Hier dürft ihr ja alle Zahlen außer die 0 einsetzen. Also kann auch alles rauskommen, außer die 0, da 1 geteilt durch irgendetwas nie null sein kann!

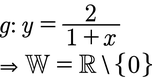
Beispiel der Wertemenge einer Funktion mit x im Nenner.

Hier genauso wie oben, was kann da alles rauskommen? Und es kann ja alles rauskommen, außer die Null, da wenn man durch 2 teilt, kann niemals Null rauskommen.

Hier kann ja alles Positive und die Null rauskommen, da wenn man die Wurzel zieht, nichts Negatives rauskommen kann.

Bei dieser Funktion kann auch alles Positive und die Null rauskommen, da wenn man etwas quadriert, das Ergebnis nie negativ sein kann.

	Was ist die Wertemenge von f(x)=x²?	Einblenden
Lösung: W=ℝ₀⁺ → Es kann bei einem geraden Exponenten schließlich jede positive Zahl rauskommen und die Null.

	Was ist die Wertemenge von f(x)=x³?	Einblenden
Lösung: W=ℝ → Hat eine Funktion einen ungeraden Exponenten, kann auch was negatives rauskommen, daher kann jede Zahl aus ℝ rauskommen.

Aufgaben und Spickzettel zur Definitions- und Wertemenge

Hier findet ihr Übungsaufgaben und Spickzettel zu diesem Thema:

Arbeitsblätter zur Definitions- und Wertemenge

Spickzettel