Asymptoten berechnen und erkennen
Folgende Inhalte helfen euch Asymptoten zu berechnen und zu erkennen:
- Erklärungen 📜
- Arten von Asymptoten und die Unterscheidung
- Senkrechte Asymptote
- Schiefe Asymptote
- Waagerechte Asymptote
- Asymptotische Kurve
- Videos 🎞️
- Arbeitsblätter 📝
- Verwandte Themen 🔗
Arten von Asymptoten und die Unterscheidung
Funktionen können verschiedene Arten von Asymptoten haben. In diesem Artikel erklären wir euch, wie ihr diese erkennen könnt und wie ihr sie berechnet. Hier werden alle erklärt:
| Art der Asymptote | Wann sie vorkommt |
| Senkrechte Asymptote | Eine senkrechte Asymptote liegt an der Stelle vor, an der der Nenner null ist. |
| Schiefe Asymptote | Wenn Zählergrad genau um 1 größer ist als der Nennergrad. |
| Waagerechte Asymptote | Wenn der Zählergrad gleich oder kleiner ist als der Nennergrad. |
| Asymptotische Kurve | Wenn der Zählergrad um mehr als 1 größer ist als der Nennergrad (also wenn Zählergrad>Nennergrad+1) |
Senkrechte Asymptote
Eine senkrechte Asymptote (also eine Asymptote parallel zur y-Achse, daran könnt ihr diese erkennen) liegt an der Stelle vor, an der der Nenner null ist.
Daher ist die Berechnung leicht, einfach die Nullstelle(n) des Nenners berechnen, an der Stelle ist die senkrechte Asymptote.
Beispiel: Senkrechte Asymptote berechnen
Es soll die senkrechte Asymptote dieser Funktion bestimmt werden:
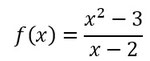
Die senkrechte Asymptote ist bei der Nullstelle des Nenners, also:

Also ist die senkrechte Asymptote bei x=2.
Hier seht ihr die senkrechte Asymptote (rot) und die Funktion (blau):

Aufgaben und Spickzettel zu senkrechten Asymptoten
Unter folgendem Button findet ihr kostenlose Aufgaben zum üben und vertiefen. Spickzettel helfen euch beim Wiederholen:
Schiefe Asymptote
Diese gibt es, wenn der Zählergrad genau um 1 größer ist als der Nennergrad. Um die Asymptote zu berechnen, geht ihr so vor:
- Teilt den Zähler durch den Nenner und rechnet dies mithilfe der Polynomdivision aus.
- Lasst dann den Restterm weg, das Ergebnis dann ist die schiefe Asymptote.
Beispiel: schiefe Asymptote berechnen
Berechnen der schiefen Asymptote dieser Funktion:
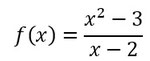
Führt die Polynomdivision durch, wobei ihr den Zähler durch den Nenner teilt:

Das blau umkreiste ist dann eure schiefe Asymptote und das Orangenfarbende ist der Restterm, den ihr dann weglassen könnt (immer das, wo das x im Nenner steht). Also sieht die Gleichung der schiefen Asymptote dann so aus:

Gezeichnet sieht dann die Funktion und die schiefe Asymptote so aus:

Waagerechte Asymptote
Eine waagerechte Asymptote liegt in zwei Fällen vor:
- Wenn der Zählergrad kleiner ist als der Nennergrad. In diesem Fall ist die x-Achse die waagerechte Asymptote
- Wenn der Zählergrad gleich dem Nennergrad ist. Dann lässt sich die waagerechte Asymptote berechnen, indem man die Faktoren vor der höchsten Potenz im Zähler durch den Faktor der höchsten Potenz im Nenner teilt.
Beispiel: waagerechte Asymptote berechnen
Die waagerechte Asymptote dieser Funktion ist gesucht. (Zählergrad=Nennergrad)

Die Asymptote ist dann an dem y-Wert, welcher sich ergibt, wenn man die Faktoren vor der gemeinsamen höchsten Potenz dividiert.
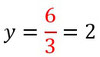
Diese Funktion und Asymptote sehen dann so aus:
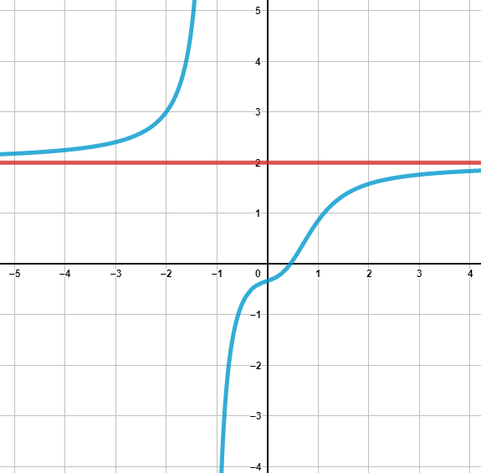
Asymptotische Kurve
Diese existiert, wenn der Zählergrad um mehr als 1 größer ist als der Nennergrad (also, wenn Zählergrad>Nennergrad+1). Eine asymptotische Kurve ist eine Asymptote, die keine Gerade, sondern eine Kurve ist, z.B. eine Parabel, die sich der Graph immer weiter annähert.
Um die Asymptote zu berechnen, geht ihr genauso vor wie bei der schiefen Asymptote:
- Teilt den Zähler durch den Nenner und rechnet dies mithilfe der Polynomdivision aus.
- Lasst dann den Restterm weg (also das, wo Rest durch Nenner steht), das Ergebnis dann ist die schiefe Asymptote.
Beispiel: asymptotische Kurve berechnen
Es wird die asymptotische Kurve für folgende Funktion gesucht (Nennergrad um 2 kleiner als der Zählergrad, also gibt es eine asymptotische Kurve):

Führt die Polynomdivision durch:
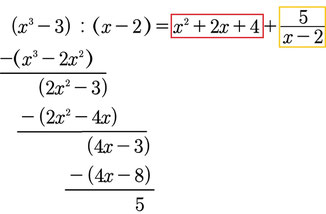
Das Rote ist dann die Gleichung der Asymptote, den Teil, mit dem x im Nenner könnt ihr weglassen, das ist der sogenannte Restterm. Also ist die Gleichung der Asymptote:
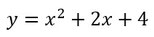
Diese Funktion und Asymptote sieht so aus:

Empfohlene Videos zu Asymptoten
ASYMPTOTEN einfach erklärt | MathemaTrick
ASYMPTOTE berechnen gebrochen rationale Funktion – Asymptoten bestimmen | MathemaTrick
Schiefe Asymptote bei Gebrochenrationalen Funktionen | Mathe by Daniel Jung
Asymptote, senkrecht, waagrecht | Fit im Mathe-Abi
