Zinsrechnung Formeln und Beispiele

Alles zur Zinsrechnung mit Formeln und Beispielen. Hier eine Übersicht der Themen:

1. Einfache Zinsrechnung (ohne Zinseszins)
   1. Jahreszins
   2. Monatszins
   3. Tageszins
2. Zinsrechnung mit Zinseszins
   1. Jahreszins
   2. Monatszins
   3. Tageszins

Mit der einfachen Zinsrechnung könnt ihr Zinsen in einem festen Zeitraum berechnen. Um beispielsweise Zinseszinsen zu berechnen, lest euch den Artikel dazu weiter unten durch. Wenn ihr etwas anderes als den Zins wissen möchtet, könnt ihr diese Formeln natürlich mit der Äquivalenzumformung umformen!

Um den Jahreszins zu berechnen, also was ihr nach einem Jahr mit dem Kapital K und Prozent p% bekommt, nutzt ihr folgende Formel:

• "Z" sind die anfallenden Zinsen nach einem Jahr (also was ihr dann dazubekommt)
• "p%" der Zinssatz (in Prozentangabe, also z.B. 10%)
• "K" das Kapital, welches verzinst wird.

Beispiel:

Ihr habt 1000€ auf dem Konto und möchtet die Zinsen nach einem Jahr mit 1% wissen, dann rechnet ihr so:

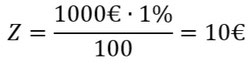
Aufgabe / Beispiel:

Den Monatszins könnt ihr mit dieser Formel berechnen:

• "Z" sind die anfallenden Zinsen nach einer bestimmten Anzahl an Monaten
• "p%" der Zinssatz
• "K" das Kapital, welches verzinst wird.
• "m" ist die Anzahl an Monaten, in welchen ihr das Kapital verzinsen möchtet. Wenn ihr z.B. die Zinsen nach 3 Monaten wissen möchtet, setzt ihr für m=3 ein.

Beispiel:

Ihr legt 120€ mit 5% an, wie viel Zinsen bekommt ihr nach zwei Monaten? Ihr rechnet dann so:

Also bekommt ihr nach zwei Monaten 1€ an Zinsen.

Tageszinsen könnt mit dieser Formel berechnen:

• "Z" sind die anfallenden Zinsen nach der Anzahl an Tagen.
• "p%" der Zinssatz.
• "K" das Kapital, welches verzinst wird.
• "t" ist die Anzahl an Tagen. Wenn ihr z.B. die Zinsen nach 3 Tagen wissen möchtet, setzt ihr für t=3 ein.

Hinweis: Man multipliziert im Nenner des Bruchs mit 360 und nicht mit 365, da es eine finanzmathematische Konvention ist, man hat sich also darauf geeignet, da dies das Rechnen erleichtert (so rechnen auch alle Banken). Falls euer Lehrer aber mit 365 rechnet, macht es so, wie er es will, da er auch eure Prüfungen bewertet 😉. 

Beispiel:

Ihr legt 120€ mit 5% an, wie viel Zinsen bekommt ihr nach 12 Tagen? 

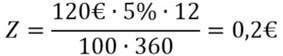
Also bekommt ihr nach 12 Tagen 20 Cent Zinsen. 

Die Zinsrechnung mit Zinseszinsen ist eine Form des exponentiellen Wachstums. Zinseszinsen sind die Zinsen, welche entstehen, wenn vorherige Zinszahlungen mitverzinst werden. Erhält man also Zinsen und werden diese bei der nächsten Verzinsung mitverzinst sind das dann Zinseszinsen.  

Hier die Berechnungen des Kapitals mit Zinseszins nach einer gewissen Zeit.

Formel für das Kapital mit Zinseszins nach t Jahren:

• K_t ist das Kapital, welches ihr nach t Jahren insgesamt habt.

• K₀ ist das Kapital, welches ihr am Anfang anlegt.

• p ist der Zinssatz, wobei ihr ihn als Dezimalzahl oder Bruch einsetzt, also z.B. 0,5=50% (Wie man das umrechnet, findet ihr unter Prozentrechnung.)
• t ist die Zeit in Jahren, die vergangen ist, bzw. der Moment, von dem ihr wissen wollt, wie viel Geld ihr habt.

Beispiel:

Möchtet ihr euer Kapital (also das Geld welches ihr besitzt) nach 5 Jahren mit einem Zins von 1% wissen, wenn ihr anfangs 300€ habt, berechnet ihr es so:

Also habt ihr nach 5 Jahren habt ihr dann 315,30€ auf dem Konto.

Aufgabe / Beispiel:

Formel für das Kapital mit Zinseszins nach t Monaten:

• K_t ist das Kapital, welches ihr nach t Monaten insgesamt habt.

• K₀ ist das Kapital, welches ihr am Anfang anlegt.

• p ist der Zinssatz, wobei ihr ihn als Kommazahl oder Bruch einsetzt, also z.B. 0,2=20% (zur Umrechnung: Prozentrechnung.)
• t ist die Zeit in Monaten, die vergangen ist, bzw. der Moment, von dem ihr wissen wollt, wie viel Geld ihr habt.

Beispiel:

Ihr legt 1200€ mit 5% (Jahreszins) an, wie Geld habt ihr nach 5 Monaten? 

Also habt ihr nach 5 Monaten mit Zinseszinsen 1224,64€.  

Um die Zinsen zu bestimmen zieht ihr das Kapital vom Beginn (1200€) vom Kapital nach 5 Monaten (1224,64€) ab, das sind dann die Zinsen (24,64€) nach 5 Jahren.

Formel für das Kapital mit Zinseszins nach t Tagen:

• K_t ist das Kapital, welches ihr nach t Tagen insgesamt habt.

• K₀ ist das Kapital, welches ihr am Anfang anlegt.

• p ist der Zinssatz, wobei ihr ihn als Kommazahl oder Bruch einsetzt, also z.B. 0,1=10% (Hier zur Umrechnung: Prozentrechnung.)
• t ist die Zeit in Tagen, die vergangen ist, bzw. der Moment, von dem ihr wissen wollt, wie viel Geld ihr habt.

Hinweis: Man teilt im Exponenten mit 360 und nicht mit 365, da es eine finanzmathematische Konvention ist, man hat sich also darauf geeignet, da dies das Rechnen erleichtert (so rechnen übrigens auch alle Banken). Falls euer Lehrer aber mit 365 rechnet, macht es so, wie er es will, da er auch eure Prüfungen bewertet 😉.  

Beispiel:

Ihr legt 1200€ mit 5% an, wie Geld habt ihr nach 50 Tagen? 

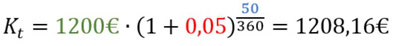
Also habt ihr mit Zinseszinsen 1208,16€ nach 50 Tagen.

• Prozentrechnung
• Potenzen
• Potenzgesetze
• Brüche und Kommazahlen umrechnen
• Exponentielles Wachstum und Zerfall

In unserem Shop findet ihr passende Lernmaterialien, z. B. Trainingsbücher mit Übungsaufgaben. Mit jedem Kauf unterstützt ihr den Betrieb unserer Webseite.