Direkte und indirekte Proportionalität
Die Proportionalität beschreibt das Verhältnis von zwei veränderlichen Größen zueinander, insofern dass wenn eine sich verändert, sich die andere ebenfalls um einen bestimmten Faktor verändert. Es gibt zwei verschiedene Arten von Proportionalität.
Klickt und scrollt direkt zur richtigen Stelle:
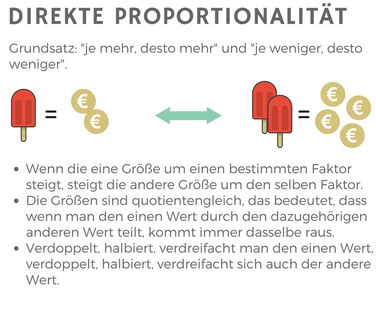

Direkte Proportionalität
Eine direkte Proportionalität hat folgende Eigenschaften:
- Wenn die eine Größe um einen bestimmten Faktor steigt, steigt die andere Größe um denselben Faktor.
-
- Beispiel: Ihr kauft 1 Schokoriegel für 1€. Dann kosten 5 Riegel 5€. Das ist eine direkte Proportionalität, denn der Betrag, den ihr bezahlen müsst, steigt genauso, wie die Anzahl eurer Riegel.
- Die Größen sind quotientengleich, das bedeutet, dass wenn man den einen Wert durch den dazugehörigen anderen Wert teilt, kommt immer dasselbe raus.
-
- Beispiel: beim selben Beispiel wie oben bedeutet es, dass wenn ihr die Anzahl an Riegeln durch die Kosten teilt, immer dasselbe rauskommt. Also 1:1€ = 5:5€.
- Verdoppelt, halbiert, verdreifacht man den einen Wert, verdoppelt, halbiert, verdreifacht sich auch der andere Wert.
- Es gilt der Grundsatz: "je mehr, desto mehr" und "je weniger, desto weniger".
-
- Je mehr Bauarbeiter, desto schneller wird ein Haus gebaut.
- Je weiniger Bauarbeiter, desto langsamer wird ein haus gebaut.
- Die direkte Proportionalität ergibt gezeichnet eine steigende Ursprungsgerade
- Aufgaben der direkten Proportionalität lassen sich meist leicht durch den Dreisatz lösen:
Proportionalitätsfaktor bei direkter Proportionalität
Der Proportionalitätsfaktor beschreibt das Verhältnis beider Werte genauer, also wie beide Werte im Verhältnis stehen. Berechnet wird dieser, für die direkte Proportionalität, so:
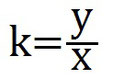
- k ist der Proportionalitätsfaktor
- y der erste Wert (z.B. was man für Wassermelonen Zahlen muss)
- x der zweite Wert, welcher zum ersten Wert gehört (z.B. Anzahl der Wassermelonen)
Dabei ist k für eine Proportionalität immer konstant, das bedeutet, man kann, um k zu berechnen, irgendwelche zusammengehörigen Werte nehmen und erhält das k für die ganze Proportionalität (es kommt ja für alle zusammengehörigen Werte immer dasselbe für k raus). Mit dem Proportionalitätsfaktor könnt ihr dann die Gleichung für diese Proportionalität angeben (k ist dabei die Steigung der Geraden), sie lautet dann:
y=k·x
Beispiel zur direkten Proportionalität
Ihr geht in einen Laden und wollt, wie typischerweise immer in Matheaufgaben, Wassermelonen kaufen ;). 1kg Wassermelonen kosten dabei 2,50€.
- Wie viel kosten dann 4kg Wassermelonen?
- Wenn man 7,50€ zahlt, wie viel Wassermelonen hat man dann gekauft?
- Was ist der Proportionalitätsfaktor?
Lösung zur Frage 1:
Hier wird gefragt, wie viel 4kg Wassermelonen kosten. Im Vergleich zu 1kg (wofür ihr den Preis gegeben habt), habt ihr jetzt 4kg an Wassermelonen. Also hat sich das Gewicht vervierfacht, so muss sich auch der Preis vervierfachen:
2,5€ · 4 = 10€
Das bedeutet, dass 4kg Wassermelonen 10€ kosten.
Diese Aufgabe könnt ihr auch mit dem Dreisatz lösen:
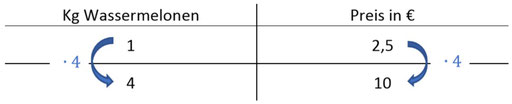
Also kosten 4kg Wassermelonen 10€.
Lösung zu Frage 2:
Nun soll man bestimmen, wie viel kg Wassermelonen man für 7,50€ bekommt. Das könnt ihr ebenfalls mit dem Dreisatz lösen:

Also bekommt man 3kg Wassermelonen für 7,50€.
Lösung zu Frage 3:
Den Proportionalitätsfaktor berechnet man, indem man eine Größe durch die Andere teilt, also:
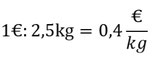
Daher ist der Proportionalitätsfaktor 0,4€/𝑘𝑔.
Die Gleichung für diese Proportionalität ist dann (eigentlich nicht gefragt, aber zur Veranschaulichung):
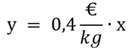
Aufgaben zur direkten Proportionalität
Hier sind zwei Aufgaben, die ihr selbst als Übung rechnen oder einfach angucken könnt. Klickt auf "Einblenden", um die Lösung zu sehen.
| 5 Tickets für das Spiel vom HSV gegen die Bayern kosten 125€. Wie viel kostet 1 Ticket? | Einblenden | |
|
Lösung: Da es eine direkte Proportionalität ist, nehmen beide Werte immer um den selben Faktor zu bzw. ab. Deshalb teilt ihr die Tickets durch 5, da dann 1 raus kommt, und ihr möchtet ja den Preis für 1 Ticket wissen. Das macht ihr auch mit dem Preis, also 125:5 und ihr erhaltet den Preis für 1 Ticket. Also kostet eins 25€. |
||
| 7 Stifte kosten 3,50€. Wie viel kosten dann 10 Stifte? | Einblenden | |
|
Lösung: Das könnt ihr am leichtesten mit dem Dreisatz lösen (Link zur Erklärung oben). Also ihr findet erstmal raus wie viel 1 Stift kostet, dazu teilt ihr den Preis und die Stiftanzahl durch 7. Dann wisst ihr, dass ein Stift 0,50€ kostet. Wenn ihr jetzt wissen möchtet, wie viel 10 Stifte kosten, müsst ihr nur noch den Preis mal 10 nehmen. Also kosten 10 Stifte 5€. |
||
Indirekte Proportionalität
Eine indirekte Proportionalität hat folgende Eigenschaften:
-
Wenn die eine Größe um einen bestimmten Faktor steigt, sinkt die andere Größe um denselben Faktor.
-
- Beispiel: 4 Arbeiter brauchen 6 Stunden zum Bemalen einer Wand, dann brauchen 8 Arbeiter nur 3 Stunden. Wie ihr seht, wurde die Anzahl an Arbeitern mal 2 genommen und die Anzahl an Stunden geteilt durch 2. Denn je mehr Arbeiter daran arbeiten, umso schneller ist die Wand fertig.
-
Die Größen sind produktgleich, das bedeutet, dass wenn man den einen Wert mal den dazugehörigen anderen Wert nimmt, kommt immer dasselbe raus.
-
- Beispiel: Anhand des Beispiels von oben seht ihr dies, denn 4·6=8·3=24
- Verdoppelt man einen Wert, so halbiert sich der andere
-
- Verdreifacht man einen Wert, so drittelt sich der Andere
- Vervierfacht man einen Wert, so viertelt sich der Andere
-
Es gilt der Grundsatz: "je mehr, desto weniger" und "je weniger, desto mehr".
- Beispiel: Je mehr Arbeiter, desto weniger Zeit brauchen sie, um etwas zu bauen.
- Beispiel: Je weniger Arbeiter, desto mehr Zeit brauchen sie, um etwas zu bauen.
-
Die indirekte Proportionalität ergibt gezeichnet eine fallende Hyperbel.
Proportionalitätsfaktor bei indirekter Proportionalität
Der Proportionalitätsfaktor beschreibt das Verhältnis beider Werte genauer, also wie beide Werte im Verhältnis stehen. Berechnen tut man diesen für die indirekte Proportionalität, so:
k=y·x
- k ist der Proportionalitätsfaktor
- y der erste Wert (z.B. Anzahl der Stunden zum bemalen einer Wand)
- x der zweite Wert, welcher zum ersten Wert gehört (z.B. Anzahl der Maler)
Dabei ist k für eine Proportionalität immer konstant, das bedeutet, ihr könnt immer irgendwelche zusammengehörige Werte nehmen und es kommt für k immer dasselbe raus. Die Einheit des Proportionalitätsfaktors ist die, welche rauskommt, wenn man die Einheiten beider Werte multipliziert. Mit dem Proportionalitätsfaktor könnt ihr dann die Gleichung für diese Proportionalität angeben, sie lautet dann:
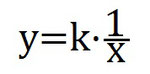
Beispiel zur indirekten Proportionalität
Der Bau des Berliner Flughafens braucht mit 1000 Arbeitern 100 Jahre.
- Wie lange würde es mit 2000 Arbeitern dauern?
- Wenn der Bau 80 Jahre dauert, wie viele Arbeiter haben dann daran gearbeitet?
- Was ist der Proportionalitätsfaktor?
Lösung zu Frage 1:
Da sich die Anzahl der Arbeiter verdoppelt, wisst ihr, dass sich nach der Definition der indirekten Proportionalität die Zeit des Baus halbieren muss, also ist der Bau mit 2000 Bauarbeitern nach 50 Jahren fertig.
Alternativ könnt ihr es auch mit einem etwas abgeänderten Dreisatz berechnen, dabei wird immer, wenn etwas geteilt wird, das andere multipliziert und umgekehrt (also nicht wie beim gewöhnlichen Dreisatz, wo immer auf beiden Seiten multipliziert oder dividiert wird):
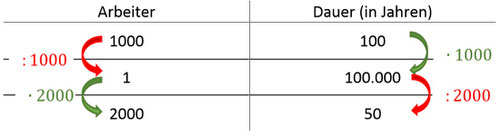
Wie ihr seht, brauchen 2000 Arbeiter 50 Jahre.
Lösung zu Frage 2:
Dies könnt ihr ebenfalls mit dem etwas abgeändertem Dreisatz, wie darüber, ausrechnen:

Also benötigt man 1250 Arbeiter, damit der Flughafen in 80 Jahren fertig ist.
Lösung zu Frage 3:
Den Proportionalitätsfaktor könnt ihr wie zwei Seiten davor beschrieben berechnen. Also zwei zugehörige Werte miteinander multiplizieren:
𝑘 = 100 ∙ 1000 = 100.000
Der Proportionalitätsfaktor ist also 100.000.
Aufgabe zur indirekten Proportionalität
Hier eine Aufgabe, die ihr selbst als Übung rechnen oder einfach angucken könnt. Klickt auf "Einblenden", um die Lösung zu sehen.
| 2 Postboten brauchen 10 Stunden, um die Briefe zu verteilen. Wie viel Stunden brauchen 4 Postboten? | Einblenden | |
|
Lösung: Hier handelt es sich um eine indirekte Proportionalität, da je mehr Postboten da sind, desto schneller tragen sie es aus. Um herauszufinden, wie lange 4 brauchen, nehmt ihr die Anzahl von Postboten mal 2, denn 2 mal 2 ist ja 4 und ihr wollt ja wissen wie lange 4 brauchen. Dann müsst ihr die Zeit, die sie brauchen durch die selbe Zahl teilen, durch die ihr die Postboten mal genommen habt, also durch 2. 10:2=5. Also brauchen 4 Postboten 5 Stunden. |
||
