Brüche kürzen - Erklärung und Beispiele
Kürzen ist eine Möglichkeit Brüche zu vereinfachen. Dabei wird der Nenner und Zähler durch einen gemeinsamen Teiler geteilt (im Beispiel durch 6), wobei der Wert des Bruches gleichbleibt, jedoch die Zahlen des Bruchs kleiner sind.

Beispiele:

Kürzen durch Wegstreichen
Man kann auch kürzen, indem man selbe Zahlen/Unbekannte im Nenner und Zähler wegstreicht (das ist dasselbe, wie durch dieselbe Zahl im Nenner und Zähler teilen, nur dass dies nicht umständlich hingeschrieben wird.). Das Vorgehen ist so:
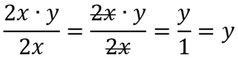
Das geht jedoch nur, wenn im Zähler und Nenner keine Summen oder Differenzen sind. Dazu gibt es den Merkspruch: „Differenzen und Summen kürzen nur die Dummen.“
Beispiele:

Aber NICHT so:

Erklärung des Kürzens
Bei den letzten beiden Beispielen könnt ihr nicht kürzen, da ihr bei einer Summe (oder Differenz) nicht kürzen dürft. Dies geht nur bei Multiplikationen! Merkt euch diesen Merkspruch:
Würde beim Kürzen eine Zahl von einem + oder – getrennt werden, darf man nicht kürzen.
Werden aber ganze Klammern multipliziert (wie bei beim letzten Beispiel von darüber), dürft ihr diese kürzen (auch wenn ein Plus drinnen vorkommt), aber nur, wenn die ganzen Klammern oder der ganze Nenner und Zähler gleich sind, denn so wird keine Zahl von einem + oder – getrennt.

Wie ihr seht, ist die Klammer oben und unten komplett identisch und diese Klammern werden multipliziert, also dürft ihr diese kürzen. Keine Zahl wird von einem – oder + getrennt.

Hier sind Nenner und Zähler komplett identisch. Jetzt dürft ihr den ganzen Nenner und Zähler kürzen. Keine Zahl wird von einem + oder – getrennt.
Aufgaben zum Kürzen von Brüchen
Hier findet ihr Aufgaben zum Kürzen in Arbeitsblättern:

