Geometrie Prüfungsteil A 2018 Bayern
Hier die original Mathematik Abiturprüfung Bayern 2018 mit dem Geometrie Prüfungsteil A.
Aufgabengruppe 1
Aufgabe 1
Gegeben ist die Kugel mit Mittelpunkt M (1|4|0) und Radius 6.
a) (3 BE)
Bestimmen Sie alle Werte p∈IR, für die der Punkt P (5 |1|p) auf der Kugel liegt.
b) (2 BE)
Die Gerade g berührt die Kugel im Punkt B (-3|8|2). Ermitteln Sie eine mögliche Gleichung von g.
Aufgabe 2
Für jeden Wert von a mit a∈IR ist eine Gerade ga gegeben durch
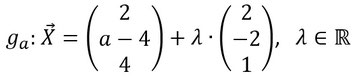
a) (2 BE)
Bestimmen Sie in Abhängigkeit von a die Koordinaten des Punkts, in dem ga die x1x2 -Ebene schneidet.
b) (3 BE)
Für genau einen Wert von a hat die Gerade ga einen Schnittpunkt mit der x3-Achse. Ermitteln Sie die Koordinaten dieses Schnittpunkts.
Aufgabengruppe 2
Aufgabe 1
Die Punkte A (1|1|1) , B (0|2|2) und C (-1| 2| 0) liegen in der Ebene E.
a) (4 BE)
Bestimmen Sie eine Gleichung von E in Normalenform.
b) (1 BE)
Geben Sie die Koordinaten des Schnittpunkts von E mit der x2-Achse an.
Aufgabe 2
Gegeben sind die Punkte A (0|0|0), B (3|-6|6) und F (2|-4|4) sowie die Gerade
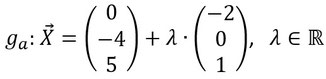
a) (4 BE)
Die Gerade h verläuft durch die Punkte A und B. Zeigen Sie, dass sich g und h im Punkt F senkrecht schneiden.
b) (1 BE)
Ein Punkt C liegt auf g und ist verschieden von F. Geben Sie die besondere Bedeutung der Strecke [CF] im Dreieck ABC an.
